Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 7

2) умножение любой строки (уравнения) на число ;

3) отбрасывание одной из двух равных или пропорциональных строк (уравнений) ;

4) прибавление к любой строке (уравнению) другой строки (уравнения), умноженной на число .

После выполнения преобразований возможны три случая:

а) 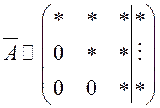. В этом случае эквивалентна треугольной матрице и

, значит, решение системы единственно. Последовательно вычисляя неизвестные снизу вверх, находим решение системы.

б) 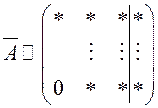. В этом случае эквивалентна трапециевидной матрице, значит, и система имеет бесконечное множество решений: () переменных перенесем вправо и будем считать их свободными (известными), тогда оставшиеся переменных определятся единственным образом как функции свободных.

в) 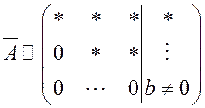. В этом случае , и система несовместна.

ПРИМЕР. Решить систему линейных уравнений: .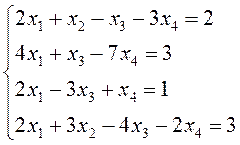

Выпишем расширенную матрицу и системы и упростим ее с помощью элементарных преобразований над строками:

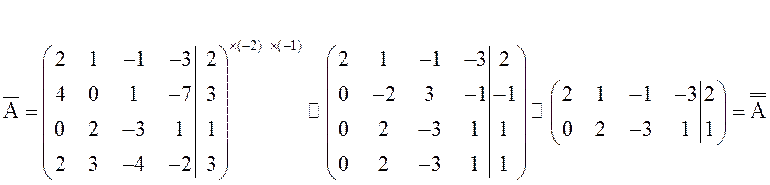
Очевидно, что 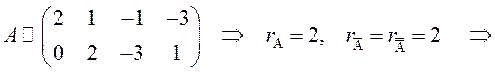по теореме

Кронекера-Капелли система совместна.

, значит, по теореме о числе решений система неопределенная, то есть имеет бесконечное множество решений и – число свободных переменных.

Выпишем систему, соответствующую матрице и эквивалентную исходной:

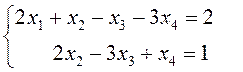Перенесем в правую часть переменные , считая их свободными ( – зависимые переменные):

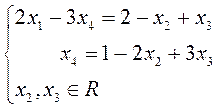Теперь подставим в первое уравнение и выразим через свободные переменные:

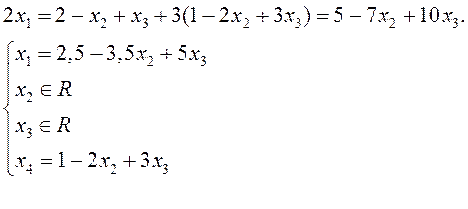– общее решение системы.

ОПРЕДЕЛЕНИЕ. Общим решением системы (1.14) называется решение, содержащее информацию обо всех неизвестных, в котором зависимые переменные выражаются как функции свободных.

Решение, полученное из общего при конкретных значениях свободных переменных, называется частным решением.

Например, частными решениями этой системы являются:

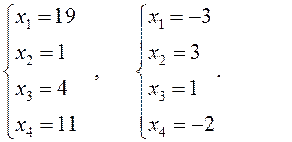
Сделаем проверку частного решения (для всех уравнений исходной системы!):

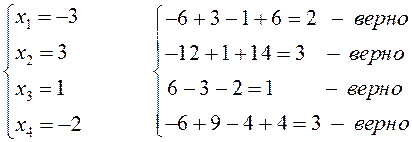Глава 2. ВЕКТОРНАЯ АЛГЕБРА

ВЕКТОРЫ И ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД НИМИ

ОПРЕДЕЛЕНИЕ. Вектором называется направленный отрезок (рис. 1).

А – начало, В – конец вектора .

Рис. 1

Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.

ОПРЕДЕЛЕНИЕ. Вектором называется упорядоченная пара точек.

ОПРЕДЕЛЕНИЕ. Длина вектора – расстояние между его началом и концом.

ОПРЕДЕЛЕНИЕ. Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.

Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.

Если начало и конец вектора совпадают, он называется нулевым:

– нулевой вектор: его направление не определено, а длина .

ОПРЕДЕЛЕНИЕ. Векторы и называются коллинеарными, если они лежат на параллельных прямых: .

Так как направление нулевого вектора не определено, то он коллинеарен любому другому.

ОПРЕДЕЛЕНИЕ. Векторы называются компланарными, если они параллельны одной плоскости.

Нулевой вектор компланарен любой системе компланарных векторов.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

Линейными называются операции сложения векторов и умножения на число.

1. СЛОЖЕНИЕ

а) Правило параллелограмма (рис.2): начала и совмещаются в одной точке, и – диагональ параллелограмма, построенного на и .

б) Правило треугольника (рис. 3): начало совмещается с концом , и направлен от начала к концу .

Рис. 2

Рис. 3

в) Правило сложения нескольких векторов (рис. 4).

Вектор замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и направлен от начала к концу .