Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 19

ВЫВОД.  Чтобы привести квадратичную форму к каноническому виду, надо:

1. Составить и решить характеристическое уравнение (3.36); его решения – собственные значения – являются коэффициентами при  и  в каноническом виде квадратичной формы.

2. Найти единичные собственные векторы, решив (3.34) и (3.35); они будут ортами новой системы координат . При этом если ось  сонаправлена с , а ось  – с , то  – канонический вид, который квадратичная форма имеет в системе .

ПРИВЕДЕНИЕ  ОБЩЕГО  УРАВНЕНИЯ 

КРИВОЙ  ВТОРОГО  ПОРЯДКА  К КАНОНИЧЕСКОМУ  ВИДУ

Общее уравнение кривой второго порядка имеет вид:

.

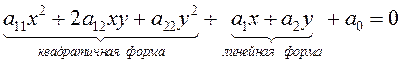В результате невырожденного линейного преобразования с матрицей   квадратичная форма перейдет в квадратичную форму, линейная – в линейную, а свободный член   не изменится. Каждую группу слагаемых будем преобразовывать отдельно, а именно: найдем ортогональное преобразование, приводящее квадратичную форму к каноническому виду, затем посмотрим, как в результате этого преобразования изменится линейная форма (ортогональное преобразование в нашем случае – это поворот осей). После поворота осей подберем параллельный перенос новой системы  так, чтобы после него уравнение кривой стало каноническим.

ПРИМЕР. Привести к каноническому виду ранее полученное уравнение параболы (стр. 58) и построить ее:

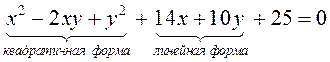.                                   (3.37)

1) Составим матрицу квадратичной формы: .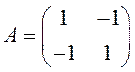

2) Составим и решим характеристическое уравнение (3.36):

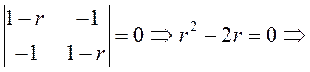
  – собственные значения.

3) Найдем первый единичный собственный вектор, то есть решим систему (3.34):

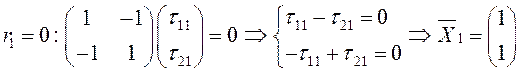 – первый собственный вектор.

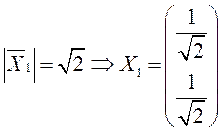 – первый единичный  собственный вектор (орт оси ).

4) Найдем второй единичный собственный вектор, то есть решим (3.35):

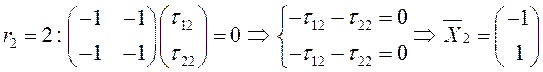 – второй  собственный вектор.

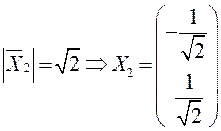 – второй  единичный  собственный вектор (орт оси .

Заметим, что , так как скалярное произведение  .

5) Запишем матрицу поворота :  . 

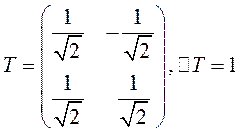Кроме того, , то есть  ортогональна. В результате преобразования с матрицей  квадратичная форма примет вид:

.

6) Выпишем уравнения, связывающие старые координаты  с новыми :

(3.32) 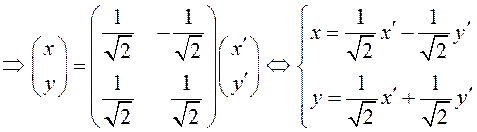 – формулы поворота координатных осей (см. 3.24).

Тогда линейная форма изменит свой вид таким образом: 

.

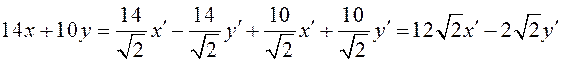Итак, в системе  кривая задается уравнением:  

. Выделим полный квадрат по переменной  :

.

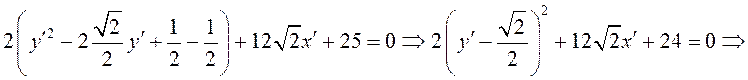
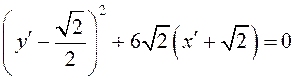7) Сделаем параллельный перенос осей в новое начало – вершину параболы: 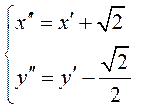  – формулы параллельного переноса осей в точку 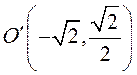 (см. 3.23). В системе  кривая задается уравнением . Это каноническое уравнение параболы.

Для того, чтобы построить параболу (3.37), надо в пдск ХОУ построить векторы    и    и вдоль них направить оси    и    соответственно. Затем сделать параллельный перенос этих осей в точку 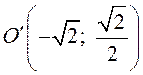 . В полученной таким образом системе координат  , взяв несколько контрольных точек, нарисуем параболу   (рис. 44).

Сравните эскиз (рис. 36) и данный рисунок, являющийся результатом точных расчетов.

y                                                                                         О                   x F                            Рис. 44

ПЛОСКОСТЬ

Покажем, что плоскость в пространстве задается в любой пдск линейным уравнением относительно трех переменных

Если  – некоторая точка на плоскости , а  – вектор, перпендикулярный ей, то, во-первых, через  перпендикулярно   проходит единственная плоскость, а, во-вторых,  для любой точки   вектор  . Таким свойством обладают только точки, лежащие на  .

Чтобы вывести уравнение плоскости, зададим в пространстве пдск . В этой системе координат .

z M A О                                 y X     Рис. 45

Пусть  – произвольная точка на  плоскости  . Тогда      и  (рис. 45). Вычислив скалярное произведение, получим:       (3.38)

Координаты точек, лежащих в плоскости , связаны соотношением (3.38). Если же , то  не перпендикулярен  , значит, координаты такой точки не удовлетворяют полученному уравнению. Поэтому (3.38) – уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.  Заметим, что это уравнение линейно относительно  Раскрыв скобки в (3.38), получим .