Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 8

ОПРЕДЕЛЕНИЕ. Разностью называется сумма вектора и вектора, противоположного : (рис. 5).

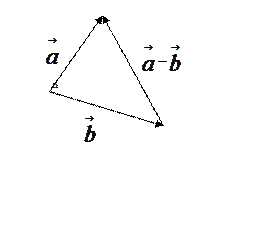Рис. 5

Начала и совмещаются в одной точке, и направлен от конца к концу .

СВОЙСТВА ЛИНЕЙНЫХ ОПЕРАЦИЙ

1.	2.
3.	4.
5.

ОПРЕДЕЛЕНИЕ. Результат конечного числа линейных операций над векторами называется их линейной комбинацией:, – линейная комбинация векторов с коэффициентами .

ПРИМЕР. Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить как линейную комбинацию

(рис. 6).

Рис. 6

. Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что .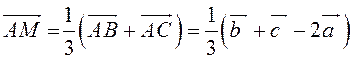

По правилу треугольника 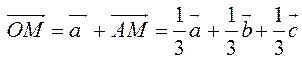, то есть – линейная комбинация с коэффициентами

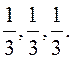
ТЕОРЕМА 1. Пусть и – неколлинеарные векторы. Тогда любой компланарный с ними вектор может быть представлен в виде

, , (2.1)

где коэффициенты (2.1) определяются единственным образом.

Представление вектора в виде (2.1) называется разложением его по двум неколлинеарным векторам.

ДОКАЗАТЕЛЬСТВО.

1. Пусть среди есть два коллинеарных, например:

2. Пусть среди коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с , а стороны п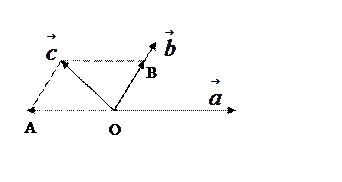араллельны прямым, на которых лежат и (рис. 7).

Тогда но

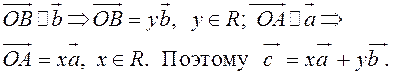
Рис. 7

Докажем единственность разложения. Предположим, что и Тогда, вычитая одно равенство из другого, получим:. Если , то 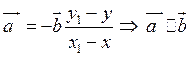, что противоречит условию. Теорема доказана.

ТЕОРЕМА 2. Пусть – некомпланарные векторы. Тогда любой вектор может быть представлен в виде

, , (2.2)

причем единственным образом.

Представление вектора в виде (2.2) называется разложением его по трем некомпланарным.

Доказать самостоятельно.

ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ.

КООРДИНАТЫ ВЕКТОРА

Осью называется направленная прямая.

ОПРЕДЕЛЕНИЕ. Ортом оси называется единичный вектор , направление которого совпадает с направлением оси.

ОПРЕДЕЛЕНИЕ. Ортогональной проекцией точки М на ось называется основание М₁ перпендикуляра, опущенного из М на .

ОПРЕДЕЛЕНИЕ. Ортогональной проекцией вектора на ось называется длина отрезка А₁В₁ этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).

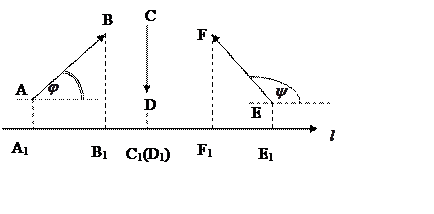Рис. 8

ОПРЕДЕЛЕНИЕ. Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).

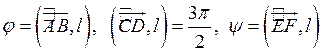(рис. 8).

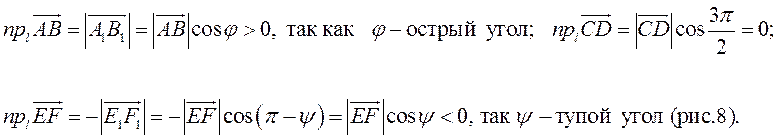
Очевидно, проекцию вектора на ось можно найти по формуле

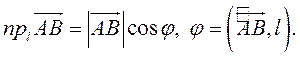
Можно показать, что проекция линейной комбинации векторов равна такой же линейной комбинации их проекций:

В частности, проекция суммы векторов равна сумме их проекций:

Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим – орт оси ОХ, – орт оси OY. Выберем точку , и пусть – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).