Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 11

а) пусть  или , или . В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что . Если , то  или , то есть .   б) пусть  или

2. .   

Доказательство: По определению направления векторов  и    противоположны, а модули равны, значит, векторы отличаются лишь знаком.

3.  – свойство линейности векторного произведения по первому сомножителю (без доказательства).

Векторное произведение также линейно и по второму сомножителю.

Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов  : векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).

Векторное произведение				Рис. 20
			-
	-
		-

Пусть  в некоторой пдск . Найдем векторное произведение этих векторов:

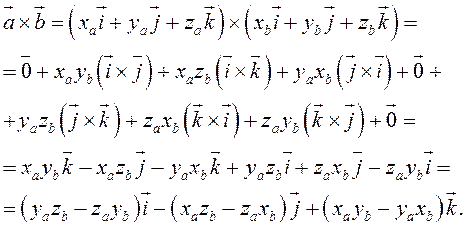
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):

.

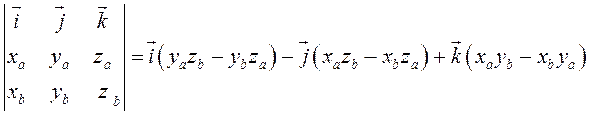Таким образом, 

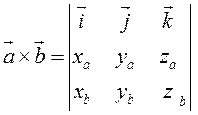.                                         (2.8)

ПРИМЕР. Вычислить векторное произведение векторов   

По формуле (2.8):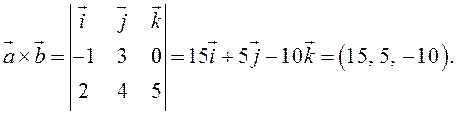 

Заметим, что площадь треугольника, построенного на векторах  и , можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что .    

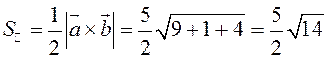
или

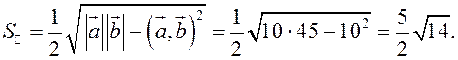
ПРИМЕР. Вычислить площадь параллелограмма, построенного на векторах    и   , если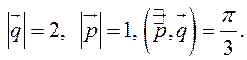

Так как  , то вычислим векторное произведение, используя его свойства: .

Отсюда  

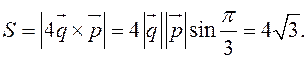
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕТОРОВ

ОПРЕДЕЛЕНИЕ. Смешанным произведением векторов  называется число  – скалярное произведение  на векторное произведение .

Смешанное произведение обозначается так:

Пусть в некоторой пдск   

Обозначим     

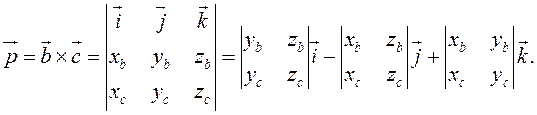
Тогда 

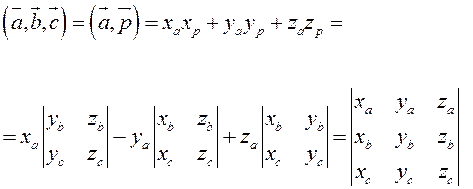  по 7 свойству определителей.

Таким образом, 

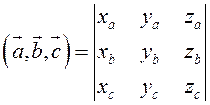                                       (2.9)

h                    S                               Рис. 21

По определению скалярного произведения Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)  – площадь параллелограмма,  – высота параллелепипеда,  – объем параллелепипеда.

Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом , если  – правая тройка, и , если  – левая тройка.

.

СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ

1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения:   компланарны 

Доказательство:  а)  компланарны    

Если   компланарны, то на них нельзя построить параллелепипед, а потому    

б)       компланарны.  

.

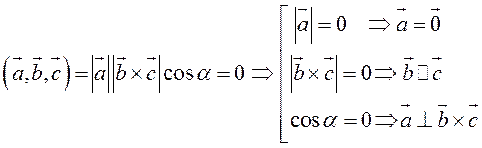Во всех трех случаях    компланарны: в частности,  если , то   параллелен плоскости векторов  , что означает их компланарность.

2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:

Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.

3. В смешанном произведении векторное и скалярное произведения можно менять местами:

Доказательство:  из свойства 2 смешанного произведения и свойства 1 скалярного получим: 

4.  Смешанное произведение линейно по каждому из трех сомножителей.

 – линейность по первому сомножителю.

Доказательство следует из формулы (2.9) и свойств определителей.

ПРИМЕР. Найти объем тетраэдра, построенного на векторах  , и его высоту, перпендикулярную плоскости векторов  и .

Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому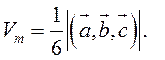  

.

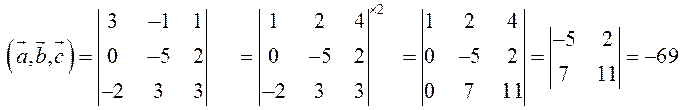Отсюда 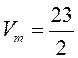 (заметим, что  – левая тройка, так как смешанное произведение отрицательно).