Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 4

ПРИМЕР.  

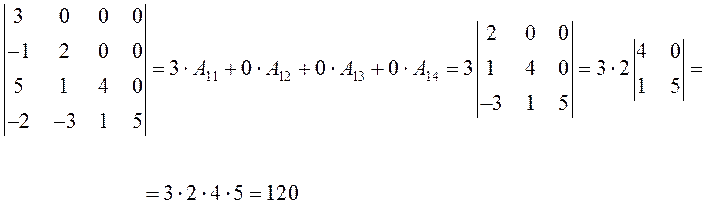
Рассмотрим (без доказательства) свойства определителей:

1.  Определитель можно разложить по элементам первого столбца:

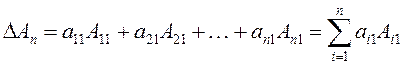                                    (1.5)

ПРИМЕР.   

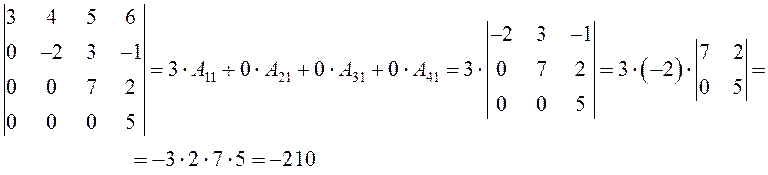
ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.

2.  При транспонировании матрицы величина ее определителя не меняется:  . 

Отсюда следует, что строки и столбцы определителя равноправны.

3.  Если в определителе поменять местами две строки (два столбца), то определитель изменит свой знак, не изменившись по абсолютной величине.

4.  Определитель, имеющий две  равные строки (столбца), равен нулю.

5.  Если все элементы некоторой строки (столбца) определителя умножить на число , то величина определителя  умножится на это число.

Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя. Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.

6.  Определитель, имеющий пропорциональные строки (столбцы), равен нулю.

7.  Определитель можно разложить по элементам любой строки (любого столбца): 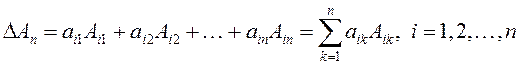            (1.6)

или   

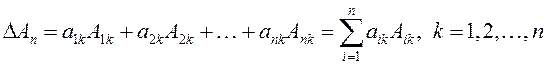                    (1.7)

Равенство  (1.6)  называется  разложением  определителя  по  элементам   -й строки.

Равенство  (1.7)  называется  разложением  определителя  по элементам -го столбца.     

8.  Сумма  произведений  всех  элементов  некоторой  строки  (столбца)  на      алгебраические дополнения соответствующих элементов другой строки

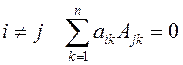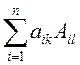(столбца) равна нулю, то есть при  и   при .

9.  Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца),   умноженных на одно и то же число.   

10. Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц:  ( – квадратные матрицы одного порядка).

ПРИМЕР. 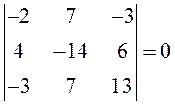 , так как элементы первой и второй строк этого определителя соответственно пропорциональны (свойство 6).

Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец,  где все элементы, кроме одного, равны нулю.

ПРИМЕР. 

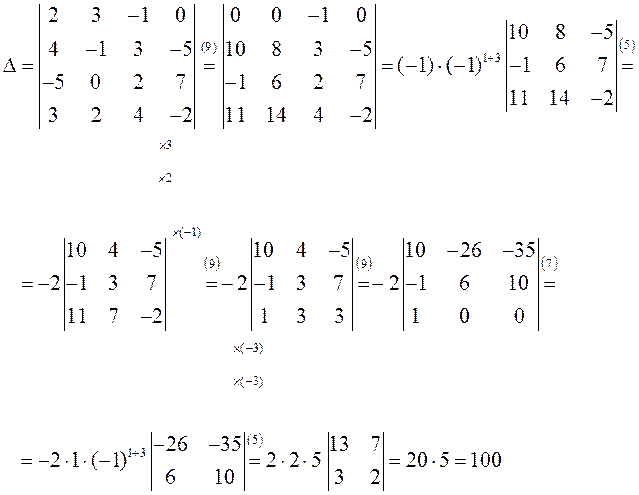
ОБРАТНАЯ МАТРИЦА

ОПРЕДЕЛЕНИЕ. Матрица  называется обратной для матрицы , если она вместе с  удовлетворяет условию: , где  – единичная матрица.

Из определения следует, что  и  – перестановочные, значит, обратная матрица существует лишь для квадратной матрицы  (прямоугольные матрицы обратных не имеют).

ОПРЕДЕЛЕНИЕ. Квадратная матрица  называется невырожденной, если . Если , то  называется  вырожденной.

ПРИМЕР.

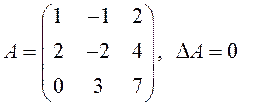по свойству 6 определителей, то есть  – вырожденная.

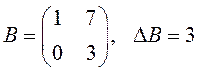, значит, – невырожденная.

ТЕОРЕМА.   Всякая невырожденная матрица имеет обратную, причем одну.

ДОКАЗАТЕЛЬСТВО.  Рассмотрим для определенности квадратную матрицу  третьего порядка:

.

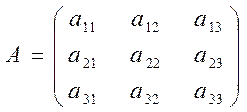Покажем, что матрица вида 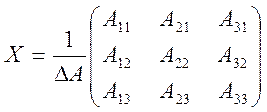 является обратной для  ( – алгебраические дополнения элементов  матрицы , ).

По условию  – невырожденная, т.е.  существует.  Найдем произведение , используя свойства 7,8 определителей:

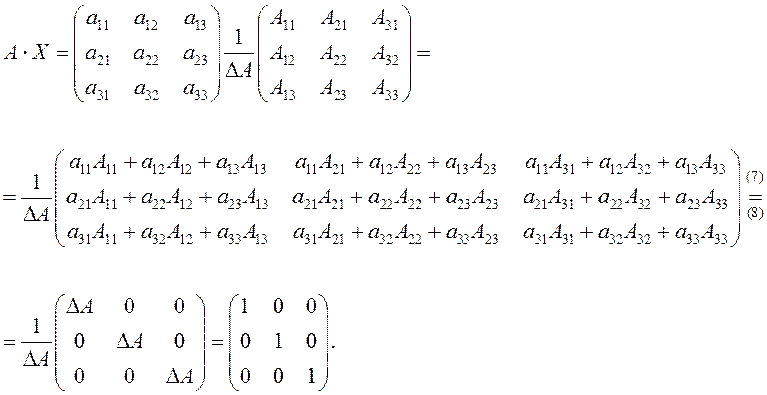
Аналогично доказывается, что .

Следовательно, по определению матрица  является обратной для .

Докажем единственность обратной матрицы.

Пусть невырожденная матрица  имеет две обратные:  и . Тогда по определению

                                                                                                     (1.8)                                                                      

                                                        (1.9)

Умножим (1.8) слева на :        .

Используя свойство 2 умножения матриц и равенство (1.9), получим:

.

Таким образом, обратная матрица единственна, что и требовалось доказать.

Обратная матрица для матрицы  - го порядка имеет вид:

.

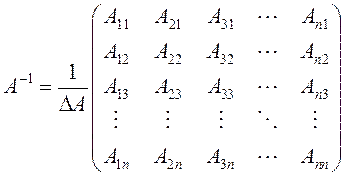ПРИМЕР. Найти матрицу, обратную для  .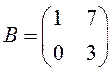     

=3 существует.  

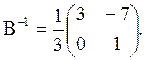
Проверка:

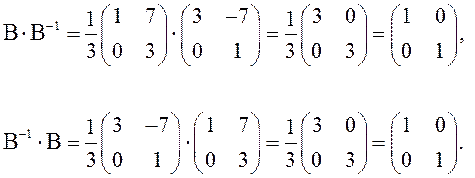
ПРИМЕР. Найти матрицу, обратную для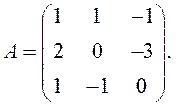         

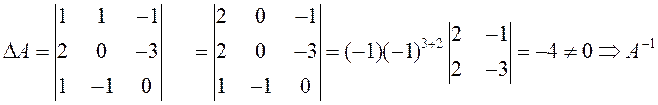 существует.

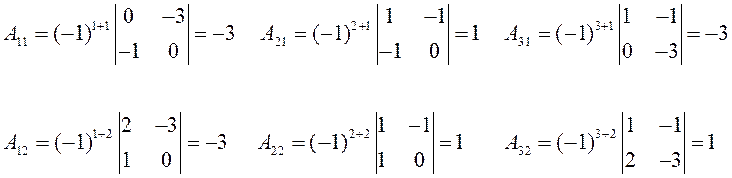
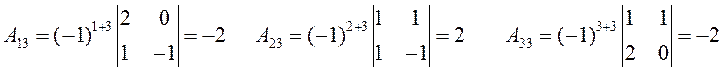
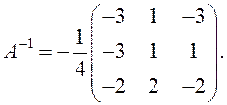
Проверка:

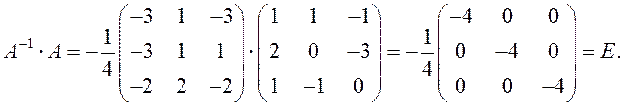
Аналогично проверяется, что .

КРАМЕРОВСКИЕ СИСТЕМЫ УРАВНЕНИЙ