Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 22

ОПРЕДЕЛЕНИЕ  ОБЩИХ  ТОЧЕК

 ПРЯМОЙ  И  ПЛОСКОСТИ

Чтобы найти общие точки прямой 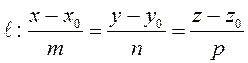  и плоскости , надо решить систему  линейных уравнений:

.

Решение этой системы будет наименее трудоемким, если перейти  к параметрическим  уравнениям прямой (3.44):

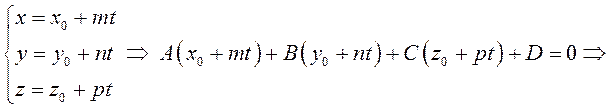
                         (3.47)

1) Пусть . Это значит, что прямая не параллельна плоскости, а потому они имеют одну общую точку. Из (3.47) найдем  

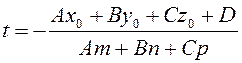
и по формулам (3.44)  – их  точку пересечения.

2) Пусть . Это означает, что в (3.47) решений нет: выполнено условие параллельности прямой и плоскости, при этом точка , но не лежит в плоскости  , значит, прямая и плоскость общих точек не имеют.

3)  Пусть 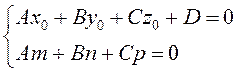. Тогда любое  – решение (3.47) и система имеет бесконечно много решений: выполнено условие параллельности прямой и плоскости и  точка  , лежащая на прямой, лежит в плоскости. Это значит, что прямая лежит в плоскости, то есть имеет с ней бесконечное множество  общих точек.

ПРИМЕР. Найти  проекцию  точки     на  плоскость   (рис. 53).

Пусть прямая    проходит через точку  М  перпендикулярно плоскости  . Точка ее пересечения с плоскостью и будет искомой проекцией. В качестве направляющего вектора    можно взять нормаль к плоскости  . Напишем канонические уравнения  прямой  (3.45):

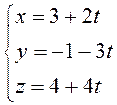.  Подставим    в уравнение плоскости:

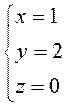, то есть  – искомая проекция.

ЦИЛИНДРИЧЕСКИЕ   ПОВЕРХНОСТИ

Уравнение  задает в пространстве некоторую поверхность.

Пусть  уравнение содержит только две переменные, например, . Рассмотренное в плоскости , оно задает некоторую кривую. Но ему будут удовлетворять и все точки пространства, которые проецируются в точки  этой кривой, так как в уравнении отсутствует , то есть все точки , у которых  х  и   у  связаны соотношением  , а  – произвольно.

ОПРЕДЕЛЕНИЕ. Цилиндрической называется поверхность, полученная движением прямой, параллельной некоторому вектору, и пересекающей при движении некоторую кривую. При этом движущаяся прямая называется образующей, а кривая, которую она пересекает, называется направляющей цилиндрической поверхности.

Для поверхности  образующая параллельна оси  (так как в уравнении  отсутствует), а направляющей является окружность в плоскости .

ВЫВОД. Если уравнение поверхности содержит только две переменные, то оно задает цилиндрическую поверхность.

У поверхности  образующая параллельна , а направляющая лежит в плоскости . Для поверхности  образующая параллельна , направляющая в плоскости .

ПРИМЕР. Построить и назвать поверхности а)    б) .

Эти уравнения задают цилиндрические поверхности. В первом случае направляющей является парабола в плоскости , а образующая параллельна  (рис. 55). Во втором – образующая синусоида в плоскости , образующая параллельна  (рис. 56).