Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 20

Обозначим , тогда уравнение (3.38) примет вид:

                                         (3.39)

(3.39) – общее уравнение плоскости в пространстве,  – ее нормаль.

ОПРЕДЕЛЕНИЕ. Любой ненулевой вектор , перпендикулярный плоскости  , называется ее нормальным вектором, или нормалью.

ОСОБЫЕ  СЛУЧАИ  РАСПОЛОЖЕНИЯ  ПЛОСКОСТИ

Выясним, какие особенности в расположении плоскости влечет за собой равенство нулю одного или нескольких коэффициентов в уравнении (3.39).

1)  координаты точки  удовлетворяют уравнению, значит, плоскость проходит через начало  координат.

2) , так как . Но , значит, плоскость .

3) , так как . Значит, плоскость .

4) , так как . Значит, плоскость .

5)  проходит через .

6)  проходит через .

7)  проходит через .

8) 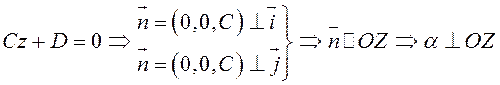 или .

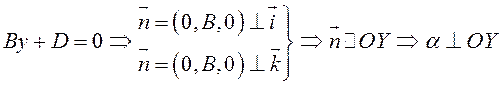9)  или .

10) 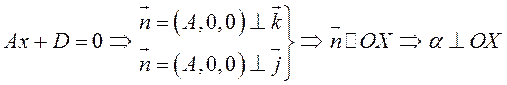 или .

11)  – плоскость .

12)  – плоскость .

13)  – плоскость .

УРАВНЕНИЕ  ПЛОСКОСТИ  В  ОТРЕЗКАХ

Пусть плоскость  не параллельна ни одной из координатных осей и не проходит через начало координат. Тогда она отсекает на координатных осях отрезки  (рис. 46). Выведем уравнение  такой плоскости.

z    C  c О            B                 y A                       b a x Рис. 46

Рассмотрим  –общее уравнение плоскости. Так как     , то . Аналогично    ;

.

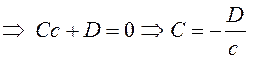Подставив А, В, С в общее уравнение, получим

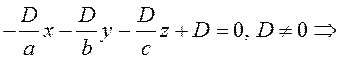
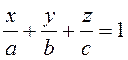                                                                                                       (3.40)

(3.40) – уравнение плоскости в отрезках.

ПРИМЕР. Вычислить объем тетраэдра, образованного плоскостями 

z 3                 -6                  О               4    y х Рис. 47

Перепишем уравнение плоскости в виде (3.40):   – уравнение данной плоскости в отрезках. Поэтому (рис. 47) .

УРАВНЕНИЕ ПЛОСКОСТИ,  ПРОХОДЯЩЕЙ 

ЧЕРЕЗ  ТРИ  ТОЧКИ

Пусть в некоторой пдск заданы три точки, не лежащие на одной прямой: . Известно, что через них проходит единственная плоскость  .

Чтобы вывести  ее уравнение, рассмотрим произвольную точку этой плоскости  . Тогда  – компланарные векторы, и их смешанное произведение равно нулю: . Тогда по формуле (2.9) получим

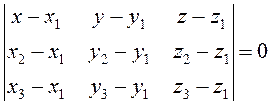                                                                                (3.41)

(3.41) – уравнение плоскости, проходящей через три точки.

ЗАМЕЧАНИЕ. Если точки лежат на одной прямой, то векторы  и  коллинеарны и   их соответствующие координаты пропорциональны. Поэтому в определителе (3.41) две строки пропорциональны и по свойству 6 определителей он тождественно равен нулю, что означает, что  координаты любой точки    удовлетворяют уравнению (3.41). Это иллюстрация того факта, что через прямую и любую точку можно провести плоскость.

ПРИМЕР. Написать уравнение плоскости, проходящей через точки

.

.

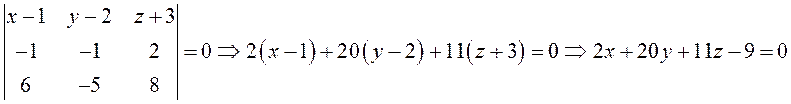УГОЛ  МЕЖДУ  ПЛОСКОСТЯМИ

ОПРЕДЕЛЕНИЕ. Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении. Если плоскости параллельны, то угол между ними равен  или  радиан.

Рассмотрим плоскости   и

.

Очевидно,                        

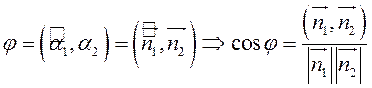
или                                  .

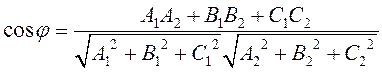Если , то  – условие перпендикулярности плоскостей.

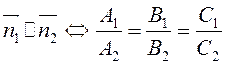Если , то  – условие параллельности плоскостей.

ПРИМЕР. Найти угол между плоскостями

.

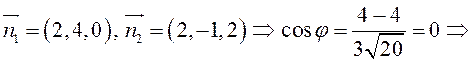 плоскости перпендикулярны.

ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕ

Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать  как результат пересечения  двух плоскостей

и

Если  не параллельна , то есть  не коллинеарен , то система уравнений

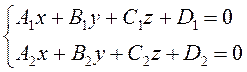                                                                           (3.42)

определяет прямую линию в пространстве.

Рис. 48

Уравнения (3.42) называются общими уравнениями прямой в пространстве. Очевидно, одна и та же прямая может быть результатом пересечения разных  пар плоскостей (рис. 48), поэтому прямую в пространстве можно задать  различными способами. Уравнения (3.42) неудобны в использовании, так как не дают представления о расположении прямой относительно выбранной системы координат.