tкр = t(a ; k), где a – заданный уровень значимости.
Если в результате сравнения окажется ôTнаблô < tкр, то нет оснований отвергнуть нулевую гипотезу H0; если же ôTнаблô > tкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
б) Н1: M(Х) < M(У)
Критическая область является левосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область), только с отрицательным знаком
tкр = – t(a; k), где a – заданный уровень значимости.
Если в результате сравнения окажется ôTнаблô< tкр, то нет оснований отвергнуть нулевую гипотезу H0; если же ôTнаблô> tкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
в) Н1: M(Х) ¹ M(У)
Критическая область является двусторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, двусторонняя критическая область)
tкр = t(a; k), где a – заданный уровень значимости.
Если в результате сравнения окажется ôTнаблô< tкр, то нет оснований отвергнуть нулевую гипотезу H0; если же ôTнабл ô> tкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
Пусть в двух генеральных совокупностях (С1 и С2) производятся независимые испытания. В результате каждого испытания событие А может появиться в первой совокупности с неизвестной вероятностью р1, во второй – с неизвестной вероятностью р2.
Имеем параметры выборок
по С1: n1 – количество испытаний; m1 – частота появления события А в этих испытаниях, w1 = m1/ n1 – относительная частота (выборочная доля) события А в совокупности С1.
по С2: n2 – количество испытаний; m2 – частота появления события А в этих испытаниях, w2 = m2/ n2 – относительная частота (выборочная доля) события А в совокупности С2.
Требуется при заданном уровне значимости a установить равенство вероятностей р1 и р2 .
Выдвинем основную и альтернативную гипотезы. Рассмотрим три случая:
а) Н0: р1 = р2 б) Н0: р1 = р2 в) Н0: р1 = р2
Н1: р1 > р2 Н1: р1 < р2 Н1: р1 ¹ р2
Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия
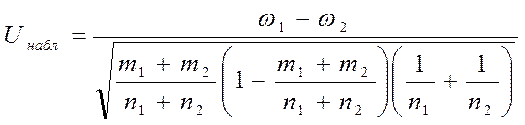
Критические области и точки зависят от выдвинутых альтернативных гипотез H1 .
а) Н1: р1 > р2
Критическая область является правосторонней. Критическая точка uкр находится из равенства Ф(uкр)= (1–2a)/2 , где функция Лапласа Ф(х) задается таблицей (приложение 2); a – заданный уровень значимости.
Если в результате сравнения окажется Uнабл < uкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Uнабл > uкр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
б) Н1: р1 < р2
Критическая область является левосторонней. Сначала находят вспомогательную точку uкр' из равенства Ф(uкр')= (1–2a)/2, тогда критическая точка равна uкр = – uкр' .
Если в результате сравнения окажется Uнабл > uкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Uнабл < uкр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
в) Н1: р1 ¹ р2
Критическая область является двусторонней. Критическая точка uкр находится из равенства Ф(uкр)= (1–a)/2 , где функция Лапласа Ф(х) задается таблицей (приложение 2).
Если в результате сравнения окажется ½Uнабл½ < uкр, то нет оснований отвергнуть нулевую гипотезу H0; если же ½Uнабл½ > uкр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
Пусть эмпирическое распределение задано интервальным статистическим рядом
|
Интервал |
х 1 – х 2 |
х 2 – х 3 |
… |
х i–1 – х i |
… |
х m –1 – х m |
|
ni |
n 1 |
n 2 |
… |
n i |
… |
n m |
Объем выборки равен n = n 1+ n 2+…+ n m .
Требуется при заданном уровне значимости a проверить, подчиняется ли генеральная совокупность выбранному теоретическому закону распределения f(x).
Выдвинем гипотезы
Н0: Признак Х подчиняется закону распределения f(x)
Н1: Признак Х не подчиняется закону распределения f(x)
Для проверки сформулированных гипотез при помощи критерия Пирсона необходимо выполнить ряд расчетов.
а) Определяют по выборке параметры выбранного теоретического распределения f(x). Пусть r - число параметров распределения.
б) Для каждого интервала Х вычисляют вероятности попадания признака Х в данный интервал. Для этого нужно использовать формулу из теории вероятности
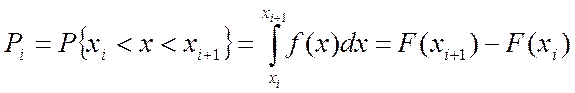 .
.
Здесь f(x) – дифференциальная функция распределения, F(x) – интегральная функция распределения. Для многих видов распределения имеются таблицы значений f(x) и F(x).
в) Определяют теоретические частоты
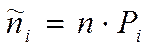 .
.
Поскольку в критерии Пирсона требуется, чтобы теоретическая частота в каждом интервале было не меньше пяти, то в противном случае допускается объединение рядом стоящих интервалов с малыми частотами.
г) Вычисляют наблюдаемое значение критерия (его еще называют критерий согласия Пирсона)
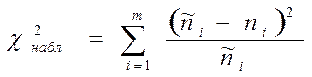 .
.
Этот критерий является случайной величиной, которая подчиняется закону распределения χ2 (хи-квадрат). Число степеней свободы равно k = m – r – 1, где m – число интервалов статистического ряда после объединения.
д) По таблице критических точек (приложение 5) находят критическое значение критерия
χ2кр = χ2 (a ; k) .
е) Если в результате сравнения окажется χ2набл < χ2кр, то нет оснований отвергнуть нулевую гипотезу H0; если же χ2набл > χ2кр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.