Математика \ Математическая статистика

Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 6

 Если выборка представлена статистическим рядом с равноотстоящими вариантами или интервальным статистическим рядом с равными интервалами разбиения, то целесообразно для упрощения расчетов использовать метод  “условного нуля”. В этом случае выбирают в качестве  “условного нуля” одну из вариант С, стоящую в центре ряда и имеющую наибольшую частоту.  Затем переходят к условным вариантам по формуле  ui = (xi –C)/h и заполняют специальную таблицу.

Таблица 6.

i

Интервалы

Середина xi

ni

ui

ni× ui

ni× ui2

ni× (ui + 1)2

1

2

…

итого

А

В

С

Д

Для проверки правильности вычислений используется тождество: åni(ui+1)2 = åniui2 + 2åniui + n  .

Из таблицы находятся условные моменты:

М1 = åniui / n  ;      М2 = åniui2 / n .

Выборочная средняя равна:  = М1·h + C

Выборочная дисперсия равна:

Dв = [M2  - (M1)2] ·h2  .

2.2.4    Задача 1. Точечные оценки

В качестве примера расчета оценок параметров распределения продолжим решение задачи 1, пункт 3.

      Определим числовые характеристики выборки по признаку Х.

 Выберем условный нуль из статистического ряда  признака Х (табл.4)  С = 1,2 .

Переходим к условным вариантам  по формуле: ui = (xi –1,2)/h , где h = 0,1.  Далее заполняем специальную таблицу.

Таблица 7

i

Интервалы

xi

ni

ui

ni× ui

ni× ui2

ni× (ui + 1)2

1

0,85-0,95

0,9

6

-3

-18

54

24

2

0,95-1,05

1

7

-2

-14

28

7

3

1,05-1,15

1,1

20

-1

-20

20

0

4

1,15-1,25

1,2

6

0

0

0

6

5

1,25-1,35

1,3

5

1

5

5

20

6

1,35-1,45

1,4

3

2

6

12

27

7

1,45-1,55

1,5

3

3

9

27

48

50

-32

146

132

Для проверки правильности вычислений используем тождество:

 åni(ui+1)2 = åniui2 + 2åniui + n

Подставляя из таблицы значения сумм

132 = 146 + 2·(–32) + 50.

Из таблицы находим условные моменты:

М1 = åniui / n = -32/50 = –0,64;

М2 = åniui2 / n = 146/50 = 2,92;

Выборочная средняя равна:=М1·h +C =  –0,64×0,1+1,2= 1,136.

Выборочная дисперсия равна:

Dв = [M2  - (M1)2]·h2  =  [2,92 – (-0,642]·0,12  =  0,025104

Выборочное среднее квадратическое отклонение равно

 0,158442

Вычислим исправленную выборочную дисперсию

S 2 = 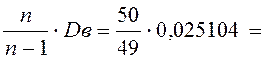 0,02562 ;

Вычислим исправленное выборочное среднее квадратическое отклонение:

 0,160.  Обозначим результат  S x = 0,16 .  

Полученные результаты позволяют сделать следующие выводы.

Средняя мощность пласта по выборке равна 1,14 м. Средний разброс мощности пласта  вокруг среднего по выборке равен 0,16 м.

Аналогично  определяем  числовые характеристики выборки по признаку У.   Выберем условный нуль С = 8,38 ; h = 1,48.

Таблица 8.

i

интервалы

уi

ni

ui

ni× ui

ni× ui2

ni× (ui + 1)2

1

3,2 - 4,68

3,94

5

-3

-15

45

20

2

4,68 - 6,16

5,42

12

-2

-24

48

12

3

6,16 - 7,64

6,9

14

-1

-14

14

0

4

7,64 - 9,12

8,38

10

0

0

0

10

5

9,12 - 10,6

9,86

4

1

4

4

16

6

10,6 -12,08

11,34

3

2

6

12

27

7

12,08 -13,56

12,82

2

3

6

18

32

итого

50

-37

141

117

åni(ui+1)2 = 117;  åniui2 = 141; åniui = –37,   n = 50

     117 = 141 + 2·(–37) + 50  –  верно.

Из таблицы находим условные моменты:

М1 =  -37/50 = –0,74;   М2 = 141/50 = 2,82.

Выборочная средняя равна:

 =М1·h +C =  –0,74×1,48+8,38= 7,2848.

Выборочная дисперсия равна:

Dв = [M2  - (M1)2]·h2  =  [2,82 – (-0,742]·1,482  = 4,97746.

Выборочное среднее квадратическое отклонение равно

 2,23102 .

S 2 = 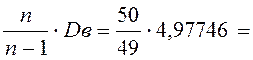 5,07905 ;

 2,25367 .

Обозначим результат  S у = 2,25367 .

Полученные результаты позволяют сделать следующие выводы.

Средняя производительность труда рабочего очистного забоя для струговых установок на антрацитовых шахтах  по выборке равна 7,28 тонны за выход. Средний разброс производительности труда рабочего очистного забоя для струговых установок на антрацитовых шахтах  вокруг среднего по выборке равен 2,25 тонны за выход.


3 Интервальные оценки параметров распределения

          Интервальной называют оценку, которая задается интервалом, покрывающим оцениваемый параметр генеральной совокупности. Доверительным называется интервал (a,b), который с заданной вероятностью g покрывает оцениваемый параметр генеральной совокупности. Вероятность g попадания оцениваемого параметра в доверительный интервал (a,b) называется доверительной вероятностью.

3.1    Доверительные интервалы для некоторых параметров распределения

Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении s генеральной совокупности задается формулой:

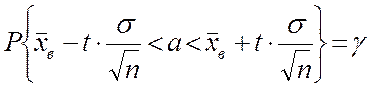 ,                                           (1)

где g = 2Ф(t) – доверительная вероятность; 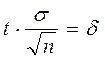  – точность оценки.

Скачать файл