Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 14

Теснота связи между результативным признаком Х и фактором У при нелинейной форме их связи оценивается при помощи коэффициента детерминации R², который находится по той же формуле (8) из  п.5.6, что и для линейной связи. Качественная оценка тесноты связи производится по шкале Чеддока.

          Аналогом коэффициента корреляции для нелинейного случая служит корреляционное отношение   .

5.8 Множественная регрессия

          Поскольку в горном деле важные производственные показатели  чаще всего объясняются несколькими факторами, то для  их прогноза применяется множественная регрессия, параметры которой определяются также по методу наименьших квадратов.

Общий вид модели:   , 

где  х₁, х₂, …, х_k   – независимые факторы, а  у – результирующий показатель. При этом функция множественной регрессии   может быть как линейная, так и нелинейная.

Очень важным является вопрос о том, сколько независимых факторов может быть в уравнении множественной регрессии при заданном объеме выборки n. Обычно используют такое правило: число наблюдений должно быть  не менее чем в 8-10 раз  больше числа факторов в уравнении регрессии.

          Наиболее удобная форма расчета линейной множественной регрессии – матричная. Приведем расчетные формулы, которые можно легко реализовать   в компьютере при помощи пакета программ Mathcad.

Пусть искомое уравнение регрессии имеет вид:  .

Введем  матрицу оценок параметров регрессии 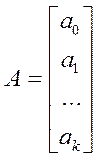 . Она неизвестна.

Для составления регрессии возьмем выборку объема n  и  запишем наблюдаемые значения  признаков  Х₁, Х₂, …, Х_k   и  У. 

На основании  полученных данных запишем матрицы:

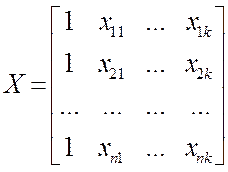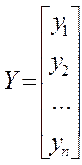 ,        . Здесь  х_ij  обозначает наблюдаемое значение i - го  признака для  j-го наблюдения.

В матричной форме уравнение регрессии имеет вид:  Х×А = У

Умножим обе части уравнения слева на транспонированную матрицу Х^Т.

Получим:  Х^Т×Х×А = Х^Т ×У.  Обозначим матрицу моментов В = Х^Т×Х. Тогда из матричного уравнения  В×А = Х^Т ×У можно найти матрицу оценок:

                                      А = В^–1 × (Х^Т ×У).

Расчет коэффициента детерминации производится по формуле:

    .

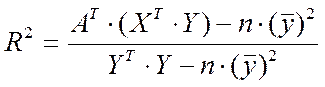Корреляционное отношение находится по формуле:    .

Проверка модели на адекватность осуществляется по критерию Фишера: 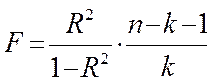     ,  где n  – объем выборки,  k  –  число переменных в уравнении регрессии. Затем по таблице критические точки распределения  Фишера – Снедекора (Приложение 7) находим критическое значение критерия

                                             F_кр = F(a , k₁ , k₂),

где a - значимость ошибки первого рода, k₁ = k , k₂, = n – k –1.

Если наблюдаемое значение критерия F окажется больше критического, то признаем полученную множественную регрессию адекватной;  если  же наблюдаемое значение критерия F окажется меньше критического,  то делаем вывод, что построенная модель не адекватной реальной.

Замечание 1   Данный способ проверки модели на адекватность можно применять и для двумерных как линейных, так и нелинейных моделей.

Замечание 2   Матричный подход в составлении уравнения регрессии можно также использовать  для случая линейной регрессии с одной переменной.

         Рассмотрим пример составления множественной регрессии.

Задача. Исследуется  зависимость месячной добычи угля по участку от мощности разрабатываемого пласта и глубины проведения работ.

Введем обозначения факторов: 

У – месячная добыча угля;  Х₁ – мощность пласта, Х₂ – глубина проведения работ.

Используя физическую сущность факторов, определим зависимые и независимые признаки.

Результативный (зависимый) признак – У ;

независимые признаки –   Х₁   и   Х₂ .

Исходные данные по 20 лавам, работающие примерно в одинаковых условиях, приводятся в таблице:

i	Y, тыс.тонн	X1 ,  м	X2  ,  м
1	22,260	1,37	1080
2	27,608	1,11	698
3	14,056	0,96	895
4	22,288	1,45	400
5	21,420	1,56	952
6	25,088	1,21	550
7	56,588	1,49	402
8	31,530	1,1	406
9	35,240	1,2	508
10	29,764	1,25	480
11	21,224	1,16	730
12	23,856	1,05	450
13	46,270	1,52	420
14	19,292	0,91	750
15	10,332	0,85	1560
16	13,972	0,92	1060
17	26,656	1,1	490
18	16,744	1,05	762
19	24,360	0,96	460
20	38,640	1,33	545

В данной задаче объем выборки равен n = 20.

Число независимых переменных равно k = 2.

Уравнение линейной регрессии имеет вид:

               

Расчеты осуществим  при помощи пакета программ Mathcad.

Реализация расчетов всех необходимых параметров и характеристик данной задачи в среде Mathcad демонстрируется ниже.

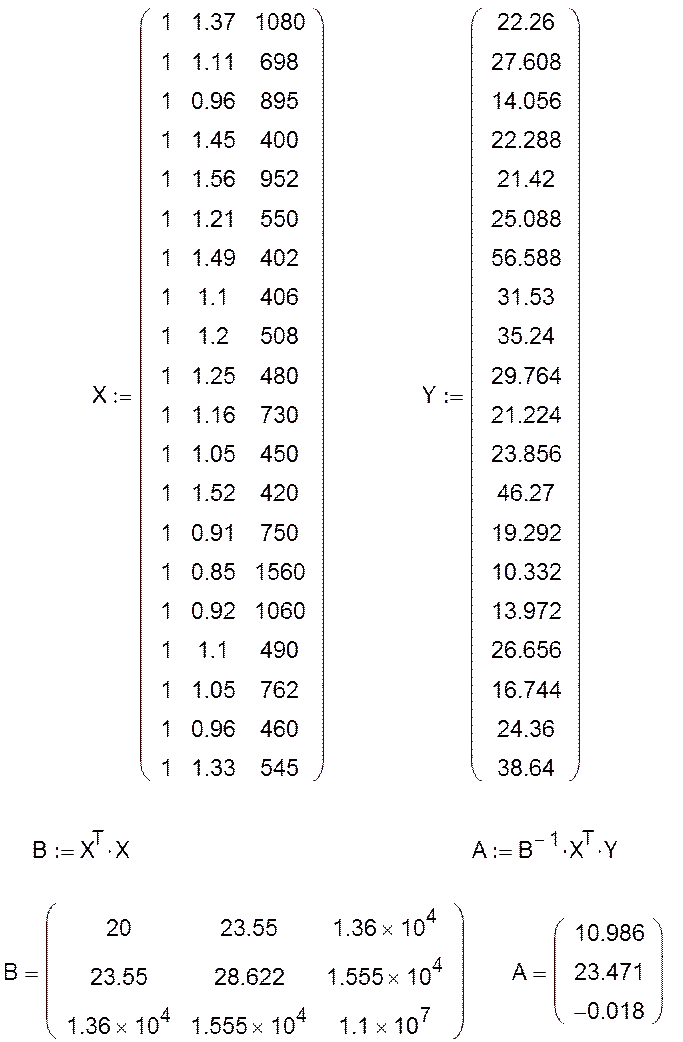
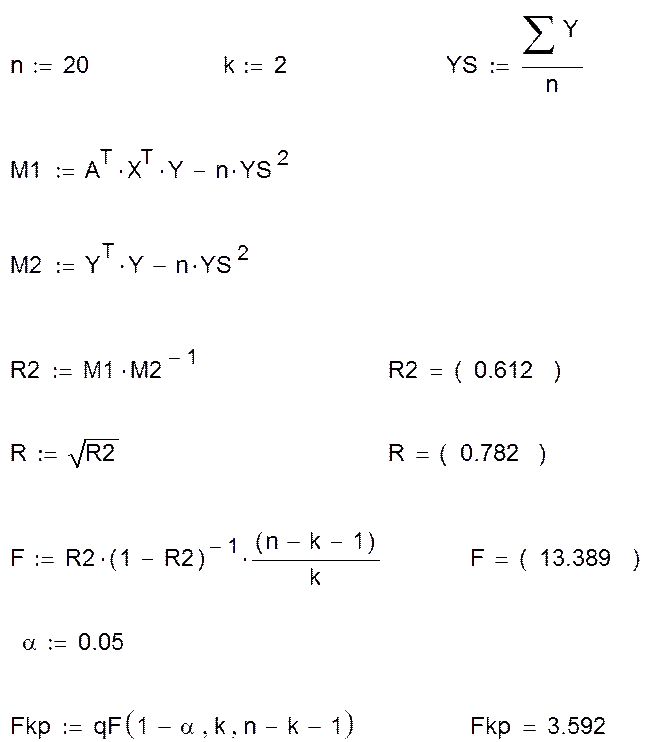
Используя результаты расчетов, сделаем выводы.

1) Уравнение линейной регрессии имеет вид:

        

Значит, с увеличением мощности пласта (Х₁)  месячная добыча угля увеличивается,  а  с  увеличением глубины работ (Х₂) месячная добыча угля уменьшается.

2) Коэффициент детерминации равен R² = 0,612. Следовательно,  вариации признаков Х₁    и  Х₂  объясняют  61,2%  общей дисперсии результативного признака  У. Остальная часть дисперсии У (38,8%) объясняется другими факторами, неучтенными в данной модели. Пользуясь шкалой Чеддока, можно утверждать, что между месячной добычей угля и независимыми факторами, такими как мощность пласта и глубина проведения работ существует заметная связь.

3) Корреляционное отношение для линейной множественной модели равно

                            R = 0,782.