Математика \ Математическая статистика

Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 16

i

X

Y

X^2

Y^2

XY

i

X

Y

X^2

Y^2

XY

1

1.13

8.4

1.2769

70.56

9.492

26

1.15

6.2

1.3225

38.44

7.13

2

1.14

7.1

1.2996

50.41

8.094

27

1.12

4.9

1.2544

24.01

5.488

3

1.13

7.7

1.2769

59.29

8.701

28

1.15

6.4

1.3225

40.96

7.36

4

1.13

7.6

1.2769

57.76

8.588

29

1.15

6.1

1.3225

37.21

7.015

5

1.14

8.2

1.2996

67.24

9.348

30

0.88

5.6

0.7744

31.36

4.928

6

1.09

6.9

1.1881

47.61

7.521

31

1.28

6.4

1.6384

40.96

8.192

7

1.53

10.9

2.3409

118.81

16.68

32

1.12

6.8

1.2544

46.24

7.616

8

1.5

11.4

2.25

129.96

17.1

33

1.2

6

1.44

36

7.2

9

1.44

13.5

2.0736

182.25

19.44

34

1.24

5.5

1.5376

30.25

6.82

10

1.39

9.5

1.9321

90.25

13.21

35

0.85

4.8

0.7225

23.04

4.08

11

1.5

9.2

2.25

84.64

13.8

36

1.21

3.5

1.4641

12.25

4.235

12

1.35

10.7

1.8225

114.49

14.45

37

1.12

10.1

1.2544

102.01

11.31

13

1.4

12.5

1.96

156.25

17.5

38

1.24

6.2

1.5376

38.44

7.688

14

1.11

7.9

1.2321

62.41

8.769

39

0.91

3.2

0.8281

10.24

2.912

15

0.91

3.7

0.8281

13.69

3.367

40

1

7.8

1

60.84

7.8

16

0.96

5.6

0.9216

31.36

5.376

41

0.94

4.1

0.8836

16.81

3.854

17

0.96

6.8

0.9216

46.24

6.528

42

1.11

5.1

1.2321

26.01

5.661

18

0.96

6.9

0.9216

47.61

6.624

43

1.13

8.5

1.2769

72.25

9.605

19

1.23

7.1

1.5129

50.41

8.733

44

1.13

8.7

1.2769

75.69

9.831

20

0.97

6.1

0.9409

37.21

5.917

45

1.33

8

1.7689

64

10.64

21

1.11

5.8

1.2321

33.64

6.438

46

0.94

6.2

0.8836

38.44

5.828

22

0.99

6.4

0.9801

40.96

6.336

47

1.2

8.3

1.44

68.89

9.96

23

1

3.4

1

11.56

3.4

48

1.1

9.6

1.21

92.16

10.56

24

1.33

8.2

1.7689

67.24

10.91

49

1.15

9.8

1.3225

96.04

11.27

25

1.15

6.5

1.3225

42.25

7.475

50

1.29

6.1

1.6641

37.21

7.869

Сумма

57.49

361.9

67.462

2873.9

428.6

Средние

1.1498

7.238

1.3492

57.477

8.5727

Из последней строки получим:

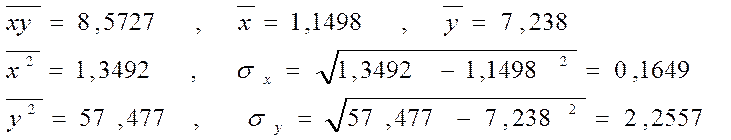
Подставив в формулу (5) пункта 2.5.4, получим:

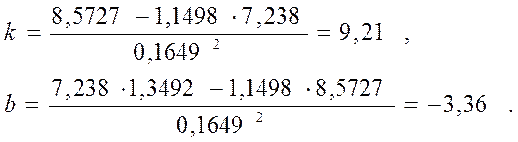
Сделаем проверку:

Следовательно, уравнение линейной регрессии имеет вид :

            = 9,21×х – 3,36

Пункт 9. Определим выборочный коэффициент корреляции по формуле

 

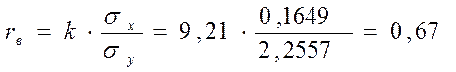
Проверим коэффициент корреляции на значимость.

Выдвинем гипотезы:

Основная гипотеза               H 0 :, rг = 0

Конкурирующая гипотеза     H 1 : rг ¹ 0.

Для проверки гипотезы H 0  вычислим наблюдаемое значение критерия:

Тнабл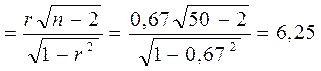

По таблице критических точек распределения Стьюдента (Приложение 6) найдем критическое значение критерия при уровне значимости a= 0,05 и числе степеней свободы k = n – 2 = 50 – 2 = 48

   tкр = tкр (0,05; 48) = 2,01. Сравнивая, получим, что Тнабл > tкр .

Следовательно, нулевую гипотезу следует отвергнуть. Это значит, что коэффициент корреляции значимо отличается от нуля  и признаки  Х  и  У коррелированны. Таким образом, у нас нет оснований отбросить гипотезу о наличии линейной корреляционной зависимости между признаками Х и У.

Пункт 10. Исходя из вида корреляционного поля и эмпирической ломаной регрессии предположим, что признаки Х и У связаны параболической зависимостью  . Для определения коэффициентов a, b, с заполним таблицу, используя  Excel.

Для краткости записей расчетную таблицу приводим не полностью.

Скачать файл