Математика \ Математическая статистика

Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 17

i

X

Y

X^2

X^3

X^4

XY

X^2Y

1

1.13

8.4

1.2769

1.443

1.6305

9.492

10.73

2

1.14

7.1

1.2996

1.482

1.689

8.094

9.227

3

1.13

7.7

1.2769

1.443

1.6305

8.701

9.832

4

1.13

7.6

1.2769

1.443

1.6305

8.588

9.704

5

1.14

8.2

1.2996

1.482

1.689

9.348

10.66

6

1.09

6.9

1.1881

1.295

1.4116

7.521

8.198

7

1.53

10.9

2.3409

3.582

5.4798

16.68

25.52

8

1.5

11.4

2.25

3.375

5.0625

17.1

25.65

9

1.44

13.5

2.0736

2.986

4.2998

19.44

27.99

10

1.39

9.5

1.9321

2.686

3.733

13.21

18.35

11

1.5

9.2

2.25

3.375

5.0625

13.8

20.7

…

…

…

…

…

…

…

…

49

1.15

9.8

1.3225

1.521

1.749

11.27

12.96

50

1.29

6.1

1.6641

2.147

2.7692

7.869

10.15

Сумма

57.49

361.9

67.4615

80.785

98.6948

428.634

518.2944

 Используя формулу (9), пункт 2.5.7, составим линейную систему:

50a+

   57,49b+

67,4615c

=

361,9

57,49a+

67,4615b+

80,7851c

=

428.634

67,4615a+

80,7851b+

98,6948c

=

518.2944

Решим систему по правилу Крамера. Вычислим главный и вспомогательные определители системы:

50

57.49

67.4615

D =

57.49

67.4615

80.7851

 = 3.8868

67.4615

80.7851

98.6948

361.9

57.49

67.4615

D1 =

428.634

67.4615

80.7851

= 21.5367

518.2944

80.7851

98.6948

50

361.9

67.4615

D2 =

57.49

428.634

80.7851

= -23.8198

67.4615

518.2944

98.6948

50

57.49

361.9

D3 =

57.49

67.4615

428.634

= 25.1881

67.4615

80.7851

518.2944

Запишем решение системы по правилу Крамера:

a = D1/D=5,541; b = D2/D=–1,128; c = D3/D=6,48.

Следовательно, уравнение нелинейной параболической регрессии имеет вид :

            = 5,541 –6,128х +6,48х2   .

Пункт 11. Построим полученные линии регрессии в одной системе координат.

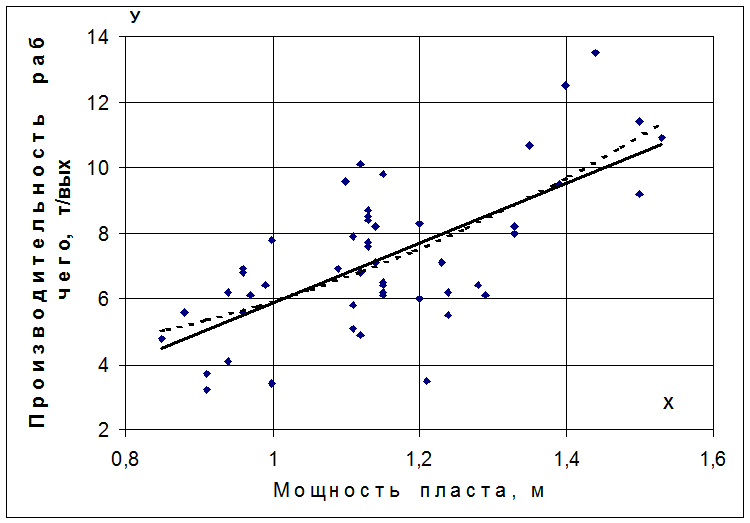
Здесь сплошная линия представляет линейную регрессию, а пунктирная линия  – параболическую регрессию.

Пункт 12. Для всех моделей рассчитаем теоретический коэффициент детерминации и теоретическое корреляционное отношение; среднюю квадратическую погрешность уравнения; среднюю относительную погрешность аппроксимации.

Используем уравнение линейной регрессии   = 9,21×х – 3,36

и параболической регрессии   = 5,541 –6,128х +6,48х2, вычислим теоретические значения признака У. Заполним таблицы.

Для краткости записей расчетные таблицы приводим не полностью.

а) Для линейной регрессии   = 9,21×х – 3,36

i

xi

уi

yiтеор

δi=yiтеор – yi

δi2

÷δi / yi÷

1

1.13

8.4

7.0473

-1.3527

1.8298

0.1610

0.0364

2

1.14

7.1

7.1394

0.0394

0.0016

0.0055

0.0097

3

1.13

7.7

7.0473

-0.6527

0.4260

0.0848

0.0364

…

…

…

…

…

…

…

…

49

1.15

9.8

7.2315

-2.5685

6.5972

0.2621

0.0000

50

1.29

6.1

8.5209

2.4209

5.8608

0.3969

1.6458

Сумма

57.49

361.9

361.4829

-0.4171

139.096

10.8476

115.3217

Для дальнейших расчетов используем формулы (8), (11), (12),

 где  Dобщ = σy2 = 2,25572 = 5,088 .

Получим:  Dобъясн уравн = 115,3217/50 = 2,306;

теоретический коэффициент детерминации

                     R2 = 2,306/5,088 =0,453

теоретическое корреляционное отношение

средняя относительная погрешность аппроксимации

      ε = 10,8476×100/50= 21,7%;

средняя квадратическая погрешность уравнения

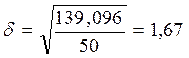      т/вых.

б) Для параболической регрессии   = 5,541 –6,128х +6,48х2

i

xi

уi

yiтеор

δi=yiтеор – yi

δi2

÷δi / yi÷

1

1.13

8.4

6.8907

-1.5093

2.2781

0.1797

0.1206

2

1.14

7.1

6.9765

-0.1235

0.0153

0.0174

0.0684

3

1.13

7.7

6.8907

-0.8093

0.6550

0.1051

0.1206

…

…

…

…

…

…

…

…

49

1.15

9.8

7.0636

-2.7364

7.4879

0.2792

0.0304

50

1.29

6.1

8.4192

2.3192

5.3789

0.3802

1.3953

Сумма

57.49

361.9

361.9018

0.0018

136.693

10.6881

117.7176
Скачать файл