Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 15

4)  Проверка модели на адекватность по критерию Фишера при уровне значимости ошибки первого рода a = 0,05 подтверждает адекватность модели, так как  наблюдаемое значение критерия F=13,389 больше критического значения  F_кр = 3,592.

5.9 Оценка погрешности модели 

          Сравнение различных моделей производится по следующим позициям:

·  по коэффициентам детерминации (теоретическим) и сравнение их с эмпирическим коэффициентом детерминации. Чем больше коэффициент R²_теор и чем ближе он к R²_эмпир, тем представленное уравнение регрессии лучше описывает зависимость между признаками Х и У.

·  По средней относительной погрешности аппроксимации:

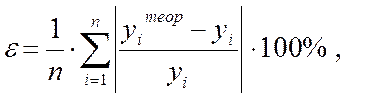                                                           (11)

 где  y_i^теор – индивидуальные значения результативного признака У, рассчитанные  по уравнению регрессии: y_i^теор=f(x_i);  у_i – значения признака У из выборки. Чем меньше средняя относительная  погрешность аппроксимации, тем модель лучше описывает зависимость между признаками. Для качественной оценки модели по относительной  погрешности аппроксимации используют следующую шкалу:

e	< 10%	10 –20%	20– 50%	50%
Вывод	Высокая точность прогноза	Хорошая точность прогноза	Удовлетворительная точность прогноза	Неудовлетворительная точность прогноза

·  По средней квадратической погрешности уравнения:

                                                      (12)

Для расчета перечисленных характеристик нужно после того, как было получено уравнение регрессии (линейное или нелинейное), заполнить следующую таблицу:

i	xi	уi	yiтеор	δi=yiтеор – yi	δi2	÷δi / yi÷
1
2
. . .
n
Сумма

5.10 Задача 1. Установления корреляционной зависимости 

Продолжим решение задачи 1. Выполним пункт 6.

 Корреляционное поле имеет вид:

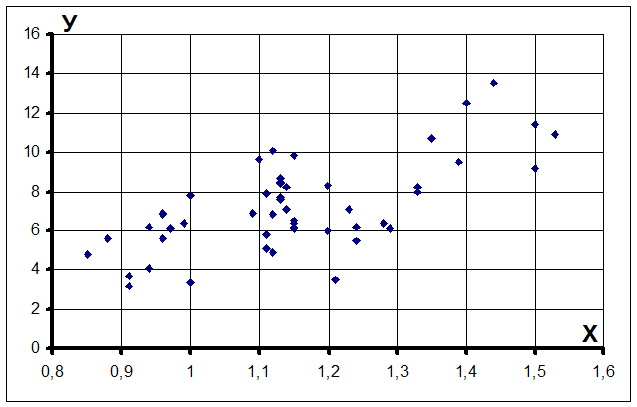
Для построения эмпирической ломаной регрессии сделаем расчет точек ,  где  х_j – середины интервалов разбиения признака Х;  – средние групповые значения признака У в каждом интервале признака Х:   = (Σ y_i)/n_j . Интервалы по признаку Х возьмем из п. 2.1.4. Заполним таблицу.

Интервал по Х	0,85-0,95	0,95-1,05	1,05-1,15	1,15-1,25	1,25-1,35	1,35-1,45	1,45-1,55
х  j	0,9	1	1,1	1,2	1,3	1,4	1,5
nj	6	7	20	6	5	3	3
у  i	4,8    5,6 3,2    3,7 4,1    6,2	5,6     6,8 6,9     6,1 6,4     3,4 7,8	6,9   9,6   5,1   5,8   7,9   4,9 6,8  10,1  7,6  7,7   8,4   8,5 8,7   7,1   8,2   6,1   6,2   6,4 6,5   9,8	6      8,3 3,5   7,1 5,5   6,2	6,4     6,1 8        8,2 10,7	9,5     12,5 13,5	9,2   11,4 10,9
	4,6	6,14	7,42	6,1	7,88	11,83	10,5

Построим эмпирическую ломаную по точкам .

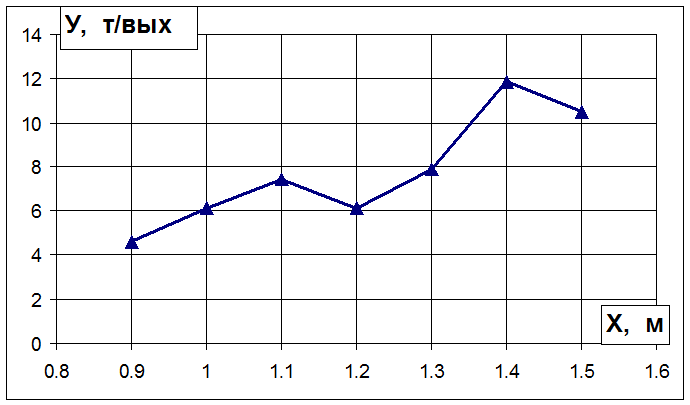
Анализ корреляционного поля и эмпирической ломаной  позволяет предполагать наличие прямой  положительной корреляционной зависимости  между признаками  Х  и  У.

          Выполним пункт 7.  Для расчета  эмпирического коэффициента  детерминации и эмпирического корреляционного отношения используем  данные  (рассчитаны в п.  2.2.4) и – средние групповые значения признака У .

Найдем межгрупповую дисперсию результативного признака У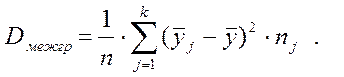

D_межгр = ((4,6–7,285)² + (6,14–7,285)² + (7,42–7,285)² +

+ (6,1–7,285)²+(7,88–7,285)²+(11,83–7,285)²+(10,5–7,285)²) =3,119

Эмпирический коэффициент детерминации равен:

 

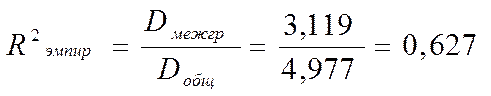
Следовательно,  62,7% вариации средней за месяц производительности рабочего  объясняется вариацией мощности  пласта.

Эмпирическое корреляционное отношение равно                  Оно указывает на значительную корреляционную связь между признаками Х и У.

Решим пункт 8.  Определим параметры уравнения линейной регрессии по формулам (3), (5), пункт 2.5.4.

С этой целью, используя исходные данные (условие задачи, пункт 2.1.4), создадим таблицу. Ее заполнение и вычисление рекомендуется выполнять в Excel.