Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 5

По результатам таблиц записываем статистические ряды для признаков Х и У.

Таблица 4. Признак Х

Интервал	0,85-0,95	0,95-1,05	1,05-1,15	1,15-1,25	1,25-1,35	1,35-1,45	1,45-1,55
х  i	0,9	1	1,1	1,2	1,3	1,4	1,5
ni	6	7	20	6	5	3	3

Таблица 5.  Признак У

Интервал	3,2- 4,68	4,68-6,16	6,16-7,64	7,64-9,12	9,12-10,6	10,6-12,08	12,08-13,56
y  i	3,94	5,42	6,9	8,38	9,86	11,34	12,82
ni	5	12	14	10	4	3	2

Графически статистические данные представляем гистограммой и полигоном относительных частот, а также кумулятой. При построении гистограммы на оси абсцисс откладывают интервалы разбиения признака Х, при построении полигона – середины интервалов разбиения признака х _i . По оси ординат  в каждом случае откладывают ординаты w_i/h.. Полученную ступенчатую фигуру называют гистограммой, ломаную линию – полигоном.

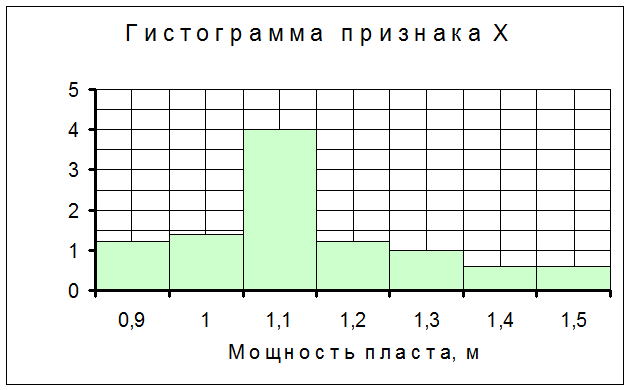
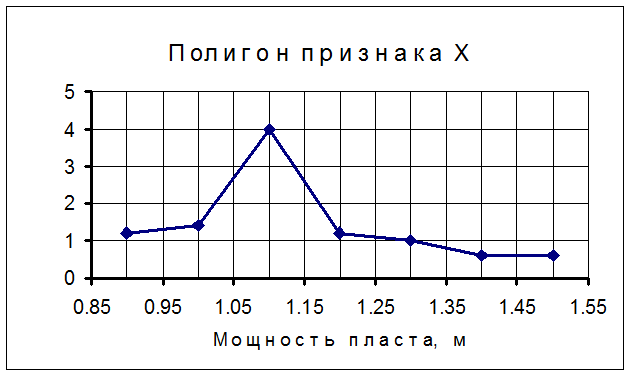
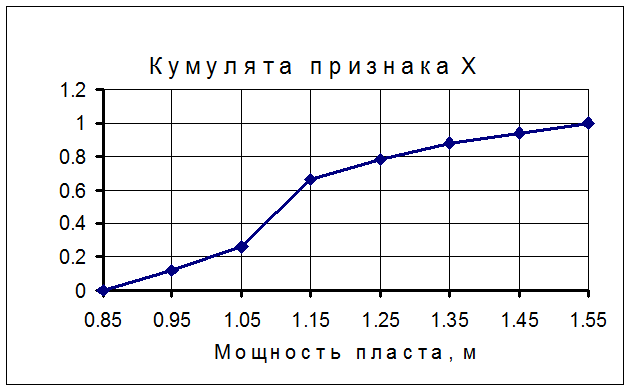
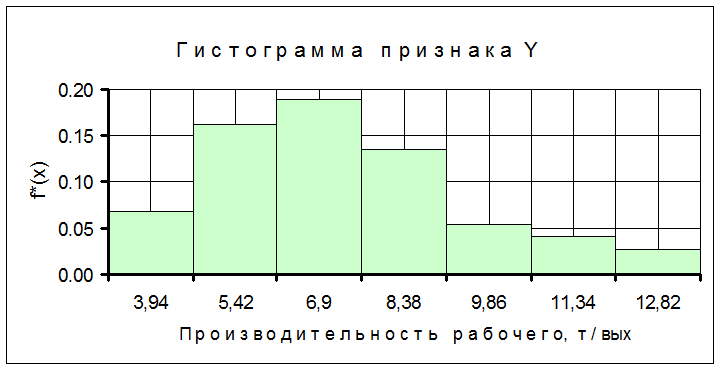
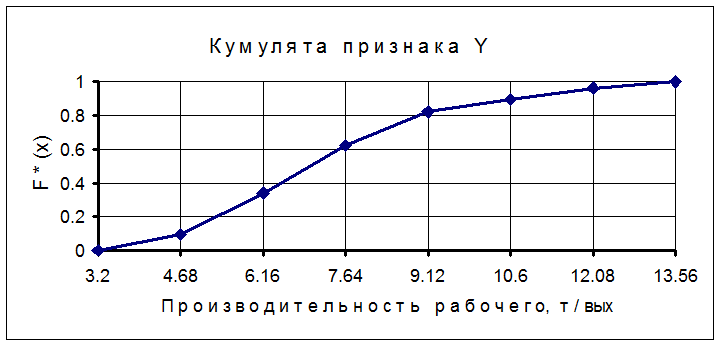
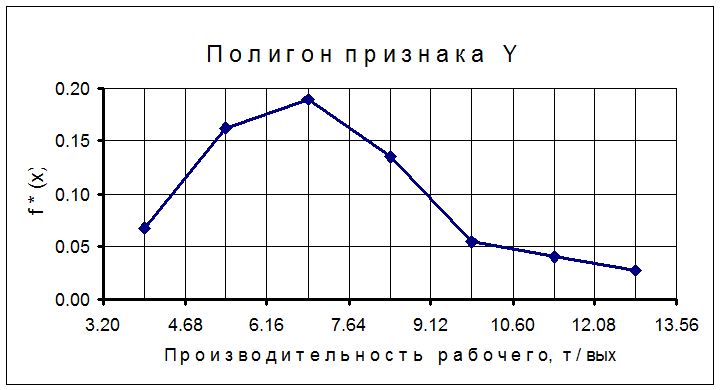2 Точечные оценки параметров распределения.

          Точечная оценка некоторого параметра распределения определяется по выборке, записывается одним числом и служит оценкой  параметра распределения генеральной совокупности. Такая оценка называется выборочной.

Приведем основные точечные оценки параметров распределения.

Математическое ожидание случайной величины оценивается по выборочной средней  ; дисперсия – по выборочной дисперсии  D_в   и исправленной выборочной дисперсии  S² ; среднее квадратическое отклонение (СКО) оценивается по выборочному среднему квадратическому отклонению s_в   и  исправленному выборочному среднему квадратическому отклонению S; асимметрия распределения оценивается по выборочному коэффициенту асимметрии А_s ; эксцесс – по выборочному эксцессу  E_к  ;  мода распределения – по выборочной  моде М_о ;  медиана распределения – по выборочной  моде М_е . Вероятность события в моделях, подчиняющихся схеме Бернулли, оценивается по выборочной доле  w .

Для трактовки полученных результатов расчета параметров выборки следует знать смысл каждой оценки. Приведем краткую их характеристику:

·   – характеризует среднее значение признака по выборке;

·  D_в   и S²  – характеризуют средний квадрат отклонения признака от среднего значения по выборке, только вторая характеристика является еще и несмещенной;

·  s_в  и  S –  характеризуют среднее отклонение признака от среднего значения по выборке;

·   А_s  –  характеризует асимметрию распределения по выборке;

·  E_к  –  характеризует “крутость” (островершинность или плосковершинность) распределения про выборке.

·  М_о  –  характеризует наиболее часто встречающуюся варианту или то значение признака, которому соответствует точка максимума плотности распределения по выборке;.

·  М_е –  характеризует то значение признака, на которое приходится середина вариационного рядя по выборке;

·  w  –  характеризует вероятность появления события А в одном испытании.

На практике для расчета перечисленных величин применяют различные формулы в зависимости от вида выборки.

   2.1 Несгруппированные статистические данные

Пусть выборка значений признака Х представляет собой не сгруппированный ряд чисел: х₁ ; x₂ ; … ; х_i ; …; x_n .

В этом случае расчет ведут по следующим формулам:

Выборочная средняя:

   ,

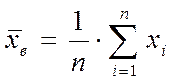Выборочная дисперсия:

  ,

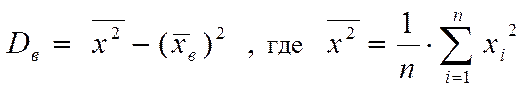Выборочное  среднее  квадратическое отклонение:

     

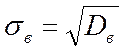
Исправленная выборочная дисперсия:

            

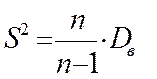
Исправленное выборочное  среднее  квадратическое отклонение:

        

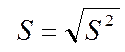
Выборочная асимметрия:

    

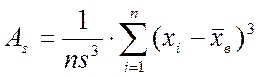
Выборочный эксцесс:

       .

2.2  Статистические дискретный и интервальный ряды

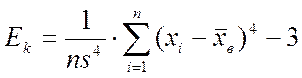 Пусть выборка задана дискретным статистическим рядом:

х  i	х  1	х  2	…	х  i	…	х  k
ni	n  1	n  2	…	n  i	…	n  k

В этом случае расчетные формулы имеют вид:

   ,

  ,

   ,    ,     ,

  ,        .

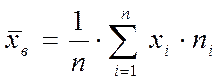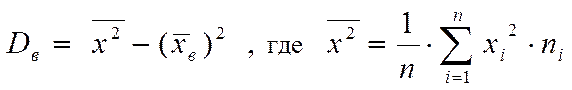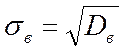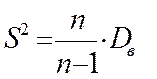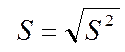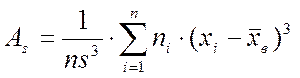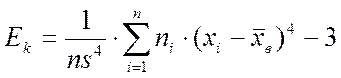Мода М_о   по дискретному ряду равна тому значению  х_m, которому соответствует наибольшая частота  n_m .

Медиана М_е   рассчитывается по вариационному (отсортированному) ряду так: если объем выборки – нечетное число  n=2m+1, то медиана равна варианте с номером m+1  в этом отсортированном ряду М_е=х_m+1 ;   если  же объем выборки – четное число  n=2m, то медиана равна  среднему арифметическому из двух центральных  вариант  М_е=0,5×(х_m + х_m+1).

Если  выборка задана интервальным статистическим рядом:

Интервал	х  1 – х  2	х  2 – х 3	…	х i–1 – х i	…	х k –1 – х k
ni	n  1	n  2	…	n  i	…	n  k

 то в этом случае заменяют интервалы их серединами  и используют формулы для дискретного ряда.

В отличие от дискретных рядов определение  моды и медианы требует проведение специальных расчетов. 

Мода  вычисляется по формуле:

                   

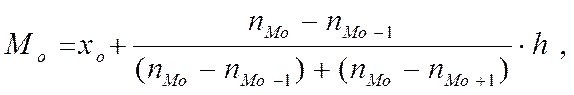
где   х₀ – начало модального интервала;

         n_Mo – частота модального интервала;

         n_{Mo -1} – частота интервала, предшествующего модальному;

         n_{Mo +1} – частота интервала, следующего за  модальным;

        h – величина модального интервала.

Медиана вычисляется по формуле:

                   

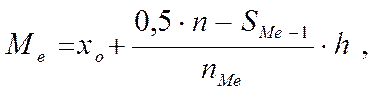
где   х₀ – начало медианного интервала;

         n_Mе – частота медианного интервала;

         n – объем выборки;

         S_{Me -1} – накопленная частота интервала, предшествующая медианному;

        h – величина медианного интервала.

2.3    Метод  “условного нуля”