Данная формула применяется для оценки математического ожидания М(Х) = а в двух случаях:
v если известно СКО – s(х)=s;
v если СКО неизвестно, но объем выборки достаточно велик (n > 30). В этом случае в качестве s берут ее оценку S.
Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении s генеральной совокупности задается формулой:
,
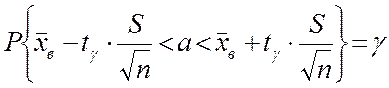(2)
где tg = t(g,n) –находят по таблице приложения 3;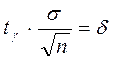 
– точность оценки.
Доверительный интервал для оценки среднего квадратического отклонения s нормально распределенного количественного признака Х задается формулой:
P{S(1 – q) < s <S(1+q)} = g , при q < 1 (3)
P{0 < s <S(1+q)} = g , при q > 1 . (4)
Здесь исправленное выборочное среднее квадратическое отклонение S служит оценкой для генерального среднего квадратического отклонения s ;
q=q(g,n) – находят по таблице приложения 4;
n – объем выборки; g – доверительная вероятность;
d = q×S – точность оценки.
Доверительный интервал для оценки неизвестной вероятности p биноминального распределения по относительной частоте w (выборочной доле) имеет вид
P{p1 < p < p2} = g , (5)
где р = Р(А) – неизвестная вероятность события А;
а концы интервала p1 и p2 определяются следующим образом:
а) Общий случай:
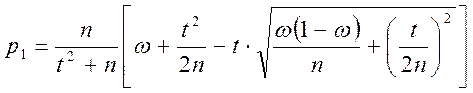(6)
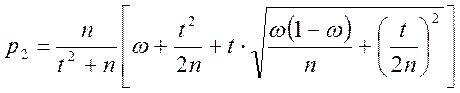
где n – объем выборки, g – доверительная вероятность;
t – находится из условия 2Ф(t) = g;
выборочная доля w находится по формуле w= m/n, где n – общее число испытаний; m – число испытаний, в которых появилось событие А.
b) Частный случай – n велико (порядка сотен):
, 
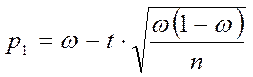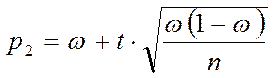(7)
с) Частный случай – известен объем генеральной совокупности N и n – велико:
,
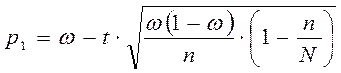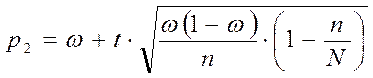(8)
Приведем примеры расчета доверительных интервалов.
Пример1.
Построим 95% доверительные интервалы для оценки математического ожидания и СКО генеральных совокупностей признака Х из задачи 1, пункт 4.
Для признака Х имеем:
= 1,14м; S = 0,16м; n =50
Для оценки математического ожидания используем формулу (2)
при g =0,95. По таблице приложения 3 находим
tg = t(0,95;50)=2,009. Подставляя в формулу (2), получим
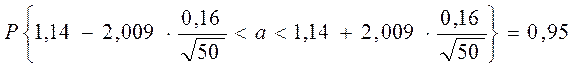
Окончательно, получим 
. Следовательно, средняя мощность
пласта по всей генеральной совокупности находится в пределах от 1,09м до 1,19м.
Надежность этого прогноза равна 95%.
Для оценки СКО по таблице приложения 4 находим
q= q(0,95;50)=0,21. Подставляя в формулу (3), получим
P{0,16(1 – 0,21) < s <0,16(1+0,21)} = 0,95.
Окончательно, получим P{0,13 < s <0,19} = 0,95. Следовательно, средний разброс мощности пласта вокруг среднего по всей генеральной совокупности находится в пределах от 0,13м до 0,19м. Надежность этого прогноза равна 95%.
Построение доверительных интервалов для признака У проводится аналогично.
Пример 2. Объединение закупает партию перфораторов в количестве 1000 шт. По предварительной договоренности объединение берет товар по цене S, если доля нестандартной продукции во всей партии не превышает 3%; если же эта доля находится в пределах от 3% до 8%, то производитель дает скидку на 10%, если доля в пределах от 8% до 20%, то предполагается скидка на 25%. При доле нестандартного товара больше чем на 20%, объединение отказывается от предложенной сделки. Для проверки качества товара была сделана выборка объемом 60 шт. Из них не прошли контроль 6 перфораторов. Следует ли объединению покупать предложенную партию, и по какой цене? При расчетах взять надежность прогноза 90%.
Пусть событие А – перфоратор оказался нестандартным.
Тогда р = Р(А) является неизвестной вероятностью, которую нужно оценить по выборке и по результатам испытаний и оценки сделать вывод о возможности и условиях сделки.
Запишем исходные данные задачи:
N = 1000; n = 60; m = 6; g = 0,9.
Выборочная доля равна w = 6/60 = 0,1.
Для построения доверительного интервала используем формулу (5), случай с).
Имеем : 2Ф(t) = 0,9. Отсюда Ф(t) = 0,45. По таблице приложения 2 находим t = 1,64. Подставляем в формулу (5) и находим верхнюю и нижнюю границы искомой вероятности:
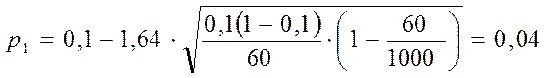
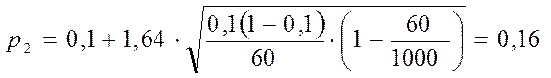
Следовательно, с надежностью прогноза 90% можно утверждать, что процент нестандартной продукции во всей закупаемой партии перфораторов находится в пределах от 4% до 16%. Значит, партию перфораторов можно купить, но при этом потребовать скидку у производителя на 25%.
Гипотеза – это высказывание предположительного характера. Под статистической гипотезой понимают гипотезу о параметрах распределения или виде функции распределения генеральной совокупности.
Примерами статистических гипотез являются следующие высказывания: генеральная совокупность, описывающая мощность пласта угля, имеет нормальный закон распределения или генеральная средняя (математическое ожидание мощности пласта) равна 1 м.
Определение. Статистическая гипотеза называется непараметрической, если в ней сформулированы предположения относительно вида функции распределения.
Определение. Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров функции распределения известного вида.
Определение. Нулевой гипотезой называют основную гипотезу и обозначают символом Но. Обычно нулевые гипотезы утверждают, что различие между сравниваемыми величинами (параметрами или функциями распределения) отсутствуют, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.