Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.
Пример. Пусть некоторому объединению, которое включает в себя 25 шахт, разрабатывающих в настоящее время 400 лав, требуется исследовать зависимость скорости подвигания очистного забоя от горно-геологических факторов. Допустим, отобрано для исследований 150 лав. Тогда объем генеральной совокупности равен N = 400, а объем выборки равен n = 150.
Различают следующие типы отборов:
Простым случайным называют такой, отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различными способами: жеребьевкой; по таблице случайных чисел.
Если выбранные объекты не возвращаются в генеральную совокупность, то выборка является простой случайной бесповторной.
Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической части». Например, пусть некоторое объединение шахт исследует вопрос надежности работы определенного оборудования. Тогда отбор показателей производят не из всей совокупности, а по каждой шахте в отдельности. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если в объединении имеются шахты с различными горно-геологическими условиями, то здесь типический отбор целесообразен.
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 10% перфораторов для выборочного контроля изношенности, то отбирают каждый десятый.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, если изделия изготовляются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.
На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы. Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.
При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен или не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект не возвращается в генеральную совокупность.
Математическая статистика позволяет получить обоснованные выводы о параметрах, видах распределений и других свойствах случайных величин по выборке, полученной из некоторой генеральной совокупности. Примем следующие обозначения: Х – изучаемая случайная величина (в статистике называется признаком); n – объем выборки; хi – наблюдаемое значение признака (варианта), ni – частота варианты хi. Статистическим рядом называется таблица, первая строка которой содержит варианты хi , а вторая строка – их частоты ni или относительные частоты (частости) ni/n. Для выборок большого объема статистический ряд может быть задан также в виде интервального ряда, который представляет собой аналогичную таблицу, но в первой строке задаются интервалы разбиения признака Х.
Очень важно, чтобы данные, полученные при статистическом анализе, были тщательно проверены и отредактированы до начала более сложного анализа. Никогда не следует забывать пословицу статистиков: «Мусор на входе – мусор на выходе».
Проверка данных может осуществляться на многих этапах статистических исследований:
· по корреляционному полю до первичной обработки данных при двумерном статистическом анализе;
· по статистическому ряду при одномерном анализе;
· по закону распределения при одномерном анализе.
Для проверки по корреляционному полю случайных величин Х и У, не разбитых на дискретные категории, необходимо построить точки в прямоугольной системе координат (х1 ;y1), (х2 ;y2), ..., (хi ;yi), …, (хn ;yn) . Полученное поле точек (диаграмма рассеяния) позволяет определить грубые ошибки и выбросы, не замеченные одномерным анализом каждой из переменных.
Для примера приведем корреляционное поле, где отмечены две точки, которые явно являются ошибочными.
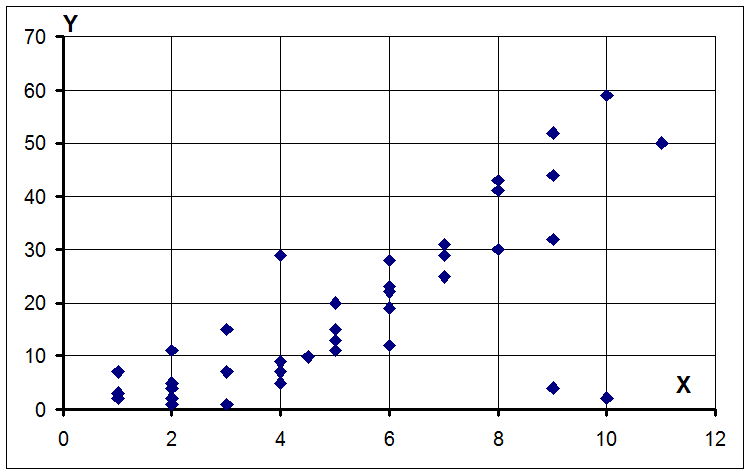

В случаях выявления подобных точек не следует автоматически исключать их из выборки. Сначала надо проанализировать ситуацию, выявить возможные пути ошибок в каждом конкретном случае, а затем принимать решение по исключению данных из выборки. Если таких точек будет много, то, возможно, их надо выделить в отдельную группу.
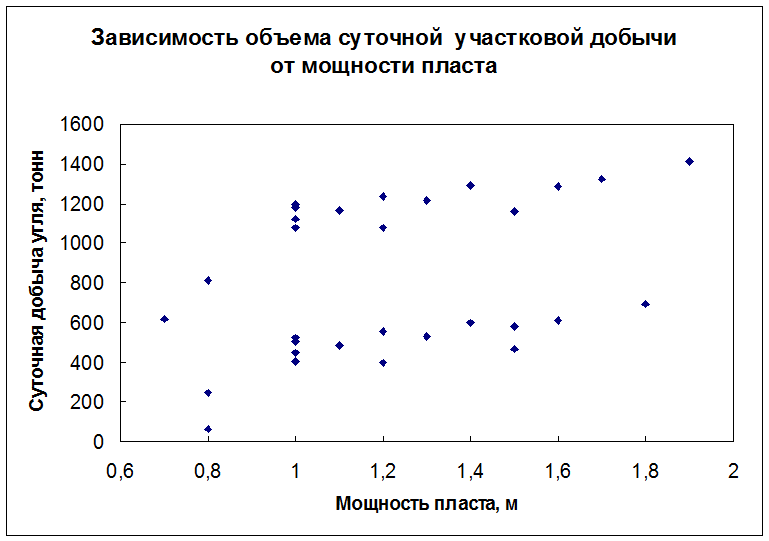
В некоторых случаях с помощью корреляционного поля можно выявить не только аномальности в числовых данных, но и установить некоторые закономерности.
Возьмем такой пример. Пусть требуется установить, как мощность разрабатываемого пласта влияет на суточную участковую добычу угля. Была взята простая случайная бесповторная выборка по ряду показателей из нескольких шахт. Построено корреляционное поле.
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.