Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 11

При уровне значимости a=0,05  проверить гипотезу о нормальном законе распределения генеральной совокупности  признака У  из задачи 1 (п. 2.3) , используя критерий Пирсона.

Проверим гипотезу о нормальном распределении признака Y. Используем критерий Пирсона.

Нормальный закон распределения является двухпараметрическим распределением с параметрами а и s. Значит,  r = 2. Из выборки по У возьмем оценки параметров распределения:

  а »  =7,284;   s » S _у = 2,254 .

Для каждого интервала признака У необходимо вычислить вероятности попадания признака  в данный интервал. Используем готовую формулу из теории вероятности для величины, распределенной нормально:

.

Здесь используются нормированная нормальная случайная величина 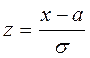  .  Функция Лапласа Ф(z )вычисляется по таблице (приложение 2). При этом учитываем, что

   Ф(–z) = – Ф(z);    Ф(– ¥) = –0,5 ;   Ф(+ ¥) = 0,5 .

В данном случае вместо случайной величины Х  берем случайную величину У.   Далее  заполним таблицу по формулам:    ;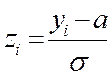  

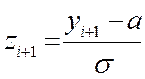
причем крайнюю левую точку интервала заменяем на  – ¥ ; крайнюю правую точку заменяем на + ¥, поскольку теоретическое нормальное распределение определено на всей числовой оси.

Теоретические частоты найдем по формуле:

 

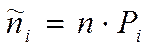
где функция Лапласа Ф(z)вычисляется по таблице (приложение 2). При этом учитываем, что     Ф(–z) = – Ф(z);    Ф(– ¥) = –0,5 ;   Ф(+ ¥) = 0,5 .

Получим таблицу:

1	2	3	4	5	6	7	8	9	10	11	12
Уi	Уi+1	ni	zi	zi+1	Ф(zi)	Ф(zi+1)	ni*	Ni*	Ni	Вi	Vi
3,2	4,68	5	– ¥	-1,16	-0,5	-0,377	6,15	6,15	5	0,21504	4,06504
4,68	6,16	12	-1,16	-0,50	-0,377	-0,1915	9,28	9,28	12	0,80061	15,5256
6,16	7,64	14	-0,50	0,16	-0,1915	0,0636	12,76	12,76	14	0,12152	15,3665
7,64	9,12	10	0,16	0,81	0,0636	0,291	11,37	11,37	10	0,16507	8,79507
9,12	10,6	4	0,81	1,47	0,291	0,4292	6,91	10,45	9	0,2012	7,7512
10,6	12,08	3	1,47	2,13	0,4292	0,4834	2,71
12,08	13,56	2	2,13	+ ¥	0,4834	0,5	0,83
Итого		50								1,50344	51,5034

После заполнения 8–го столбца отмечаем, что два последних элемента в этом столбце меньше пяти. Поскольку в   критерии Пирсона требуется, чтобы в каждом интервале было не меньше пяти единиц, то объединим частоты трех последних интервалов N_i^*  – для  8–го столбца;   N_i – для  3–го столбца.

11–ый столбец заполняем по формуле:  В_i =  .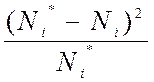

12–ый столбец – контрольный. Он вычисляется по формуле:

    V_i =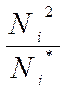 

Сделаем проверку: 50 + 1,5034 = 51, 5034.    Верно.

Заметим, что в результате проверки значения правой и левой частей могут отличатся незначительным образом.

          Запишем наблюдаемое значение критерия:  c²_набл = 1,5034.

Выберем уровень значимости ошибки  a=0,05.

Число степеней свободы равно k=m –2 – 1 , где  m  – число интервалов после объединения. В нашем случае число интервалов после объединения m= 5.   Тогда число степеней свободы равно   k=5–3 = 2.  По таблице критических точек c²  (Приложение 5) находим     c²_кр(0,05; 2)=6.

Сравниваем:         c²_набл < c²_кр .

Следовательно, нет оснований отвергнуть гипотезу о нормальном законе распределения признака Y . Поэтому принимается гипотеза о нормальном распределении признака У.

Пример 3. В результате опыта получены данные по времени безотказной работы стопора путевого ( в часах).

762	240	290	150	166	206	908	110	256	299
286	110	190	106	110	112	200	250	230	142
119	134	187	215	320	502	1246	340	365	314
390	412	473	114	596	807	220	1045	350	850

 При уровне значимости a=0,2  при помощи критерия Колмогорова-Смирнова проверить гипотезу о показательном законе  распределения генеральной совокупности  по времени безотказной работы стопора.

          Для признака Х (времени безотказной работы стопора ) определим наибольшее и наименьшее значение признака:

  X_min=106 ; X_max=1246  ;      объем выборки  n = 40.

Число интервалов разбиения определим по формуле Стэрджесса:

k =1 + 3,322× lg 40 =   6,3 .

Найдем шаг разбиения  h = (Х_max – X_min) / k.

В данном случае  h = (1246 –106) / 6,3 = 180,32. Примем  h  = 200.

Произведем группировку данных для признака Х.      

Результаты группировки представим в таблице, с помощью которой рассчитаем параметры выборки по методу “условного нуля”.

i	интервалы	хi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	100-300	200	24	-2	-48	96	24
2	300-500	400	6	-1	-6	6	0
3	500-700	600	4	0	0	0	4
4	700-900	800	3	1	3	3	12
5	900-1100	1000	2	2	4	8	18
7	1100-1300	1200	1	3	3	9	16
S			40		-44	122	74