Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 18

Отсюда получим: 

D_{объясн уравн} = 117,7176/50 = 2,354;

теоретический коэффициент детерминации

                     R² = 2,354/5,088 =0,463

теоретическое корреляционное отношение

средняя относительная погрешность аппроксимации

      ε = 10,6881×100/50= 21,4%;

средняя квадратическая погрешность уравнения

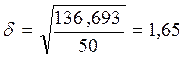      т/вых.

Сравнив результаты, можно сделать вывод, что нелинейная параболическая модель регрессии незначительно улучшает результаты, поэтому окончательно можно оставить линейную модель зависимости между мощностью пласта Х и производительностью рабочего У:  

                            = 9,21×х – 3,36.

Пункт 13. Используя линейное уравнение регрессии дадим точечный прогноз  для У  при Х = 1,8 м:       = 9,21×1,8 – 3,36 = 13,2 т/вых.

Следовательно, при мощности пласта  1,8 м  средняя производительность труда рабочего очистного забоя для струговых установок на антрацитовых шахтах прогнозируется равной 13,2 т/вых. Ошибка прогноза составляет не более 21,7% .

6  Реализация статистических расчетов при помощи компьютера

Современные компьютеры предоставляют большие возможности для расчета статистических характеристик. Отметим  наиболее приемлемые компьютерные программы и способы обработки данных в них.

6.1  Табличный процессор Microsoft  Excel   

  а) Почти ручнойсчет.  Используя простейшие средства ввода, редактирования данных в данной программе на основании приемов и формул, представленные в разделах 1-5 настоящего пособия, можно проводить статистические расчеты в любом объеме.  Этот способ хорош тем, что он позволяет пользователю создавать при помощи компьютера свой сценарий обработки данных  и дает возможность просматривать, контролировать и активно влиять на промежуточные и окончательные результаты на всех этапах решения поставленных задач. Особенно удобно представлена в этом компьютерном приложении работа с таблицами и графиками, которые, как убедился читатель, являются неотъемлемыми атрибутами статистических расчетов.  Примеры использования компьютера представленным способом приводится в разделах  1, 2 и 5.  Недостаток этого метода связан с его достоинствами и заключается в  относительно небольшой скорости расчетов и в необходимости знать все расчетные формулы (!!!).

б).  Расчет статистических характеристик при помощи встроенных функций.    В  табличном процессоре Excel в меню Вставка имеется  опция “Вставка функции” (кнопка f_х ).  При выборе этой  опции появляется диалоговое окно, разделенное на две части.

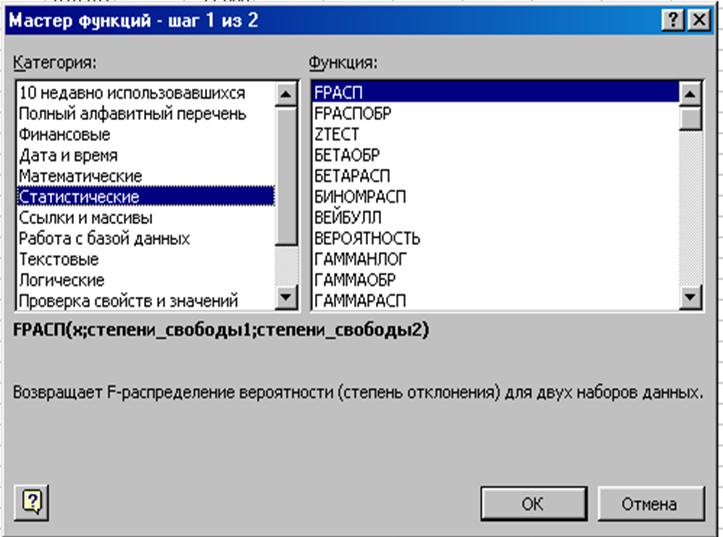
В левой части диалогового окна указываются категории функций. В нашем случае обычно выбирают категории Статистические   и  10 недавно использовавшихся.   В правой части диалогового окна выводится список функций данной категории. Если отметить какую-то функцию в этом списке, то в нижней части окна  появится формула обращения к отмеченной функции, а еще ниже приводится краткое объяснение  функции на русском языке. Если выбрать нужную функцию, то откроется соответствующее диалоговое окно. Для примера, выберем функцию КОРРЕЛ, которая позволяет вычислить коэффициент корреляции двух массивов (в нашем примере признаки Х и У):

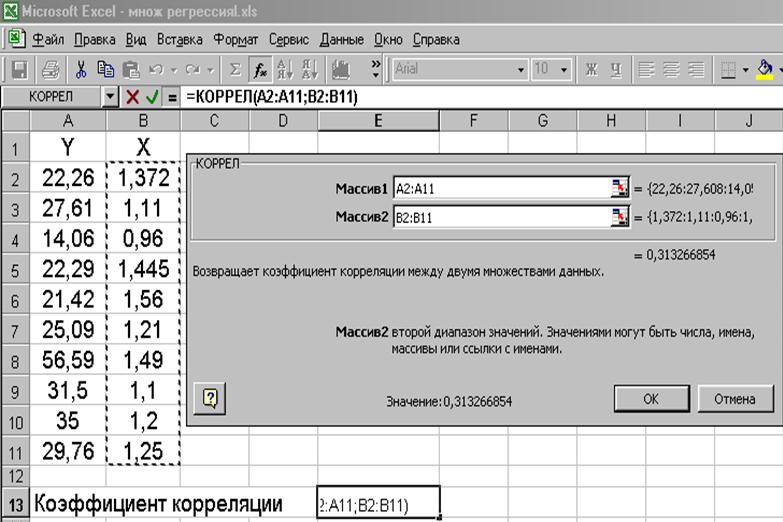
В появившемся окне нужно ввести запрашиваемую информацию. После нажатия кнопки ОК результат вычисления  записывается в ту ячейку, которая была выделена пользователем до обращения к нужной функции.

Замечание.   Если результат выполнения функции ожидается в виде массива, то вместо кнопки ОК нужно одновременно нажать три клавиши  

Ctrl+Shift+Enter .

Перечислим некоторые наиболее используемые в данном пособии функции

Название функции в статистическом анализе	Обозначение в пособии	Обращение в Excel
Выборочное среднее		СРЗНАЧ
Выборочная дисперсия	Dв	ДИСПР
Исправленная выборочная дисперсия	S2	ДИСП
Выборочное СКО	sв	СТАНДОТКЛОНП
Исправленное выборочное СКО	S2	СТАНДОТКЛОН
Выборочный коэффициент корреляции	rв	КОРРЕЛ
Параметры линейной регрессии	k, b	ЛИНЕЙН
Коэффициент  линейной регрессии	k	НАКЛОН
Свободный член регрессии	b	ОТРЕЗОК
Медиана	Ме	МЕДИАНА
Мода	Мо	МОДА
Коэффициент асимметрии	А	СКОС
Эксцесс	Е	ЭКСЦЕСС
Критические точки распределения Фишера	F	FРАСПОБР
Функция Лапласа	Ф(х)	НОРМСТРАСП – 0,5
Критические точки распределения Стьюдента	t	СТЬЮДРАСПОБР
Критические точки ХИ–квадрат распределения	c2	ХИ2ОБР

в).  Составление уравнений регрессии  y=f(x) при помощи мастера диаграмм.    В  табличном процессоре Excel в меню Вставка имеется  опция “Диаграмма”.  При выборе этой  опции появляется Мастер Диаграмм.

    

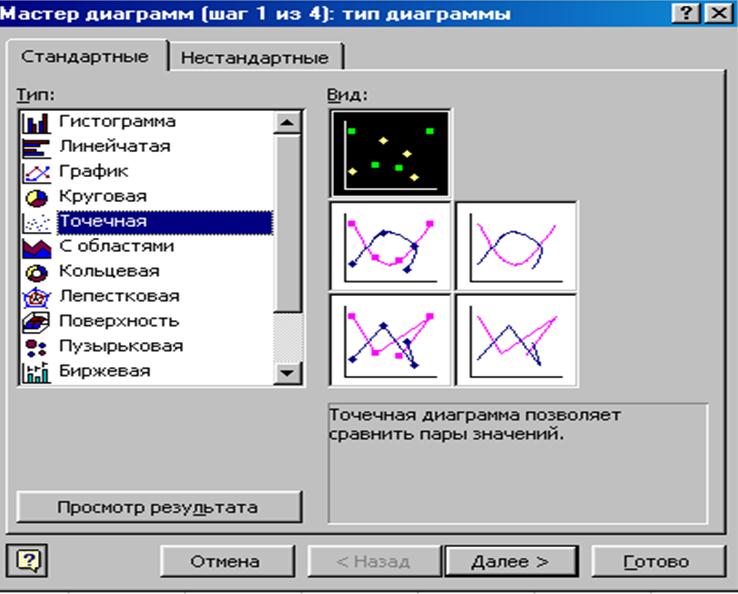
Нужно выбрать тип диаграммы – точечная; вид диаграммы -  точечный рисунок без линий соединения. Далее нужно следовать указаниям мастера и в результате получается диаграмма следующего вида:

х	у
55	5
5	70
15	40
20	30
10	60
8	50
40	10
32	15