Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 37

Отсюда получим:

 

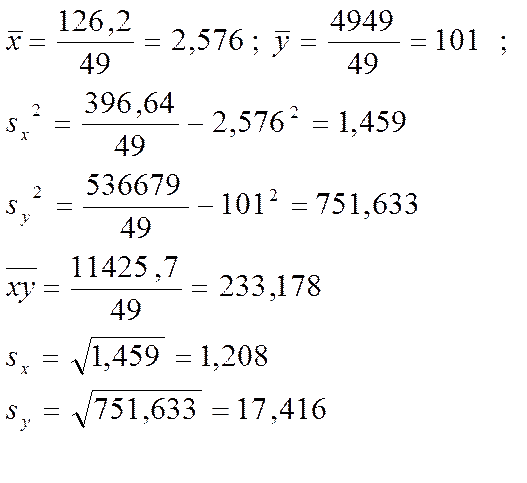
Следовательно, параметры уравнения регрессии равны:

   

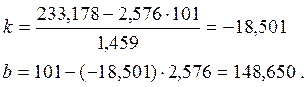
Окончательно, уравнение линейной регрессии имеет вид :

            у = –18,501×х + 148,65  .

 Определим выборочный коэффициент корреляции по формуле

  r = k×S_x / S_y . Получим  r = – 0,815.

Проверим коэффициент корреляции на значимость.

Основная гипотеза               H ₀ :, r_г = 0

Конкурирующая гипотеза     H ₀ : r_г ¹ 0.

Для проверки гипотезы H ₀  вычислим наблюдаемое значение критерия:

Т_набл 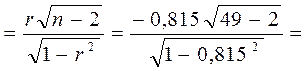 – 9,64

По таблице критических точек распределения Стьюдента  найдем критическое значение критерия при уровне значимости ошибки a = 0,05 и числе степеней свободы k = n – 2 = 49 – 2 = 47 :

t_кр = t_кр (0,05; 47) = 2,01. Сравнивая, получим, что ïТ_набл ï> t_кр .

 Следовательно, нулевую гипотезу следует отвергнуть. Это значит, что коэффициент корреляции значимо отличается от нуля, и признаки  Х  и  У коррелированы.

          Найдем коэффициент детерминации, который для случая линейной регрессии равен квадрату коэффициента корреляции: R = r²  . Получим:

   R² = (–0,815)² = 0,66. Он говорит о том, что 66% вариации величины опускания кровли объясняется вариацией скорости подвигания очистного забоя. Для определения типа связи между признаками используем шкалу Чеддока.

Для нашего случая     R² = 0,66. Поэтому на основании шкалы Чеддока делаем вывод о том, что между величиной опускания кровли и скоростью подвигания очистного забоя существует заметная  связь.

8. По уравнению регрессии       у = –18,501×х + 148,65    построим прямую в той же системе координат, что и корреляционное поле. С этой целью рассчитаем координаты двух точек:    х₁ =1 ; у₁ = 130,2

                                                    х₂  = 4 , у₂ = 74,7

Построим точки на графике и соединим их прямой. Получим линию регрессии.

9.   Вычислим погрешности уравнения регрессии.

а) Абсолютная погрешность уравнения равна:

   S_ур  =  15,879

б) Относительная погрешность  уравнения равна:

   

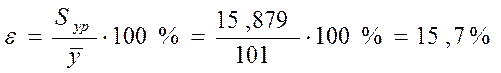
Отсюда видно, что относительная ошибка вычислений по полученному уравнению регрессии составляет 15,7%. 

10. Используем полученное уравнение регрессии для точечного прогноза  У  при X =  1,5 м/сут .

                      у_{прогноз} = –18,501×1,5 + 148,65 = 120,91 мм.

Следовательно, при скорости подвигания очистного забоя 1,5 м/сут  величина опускания кровли прогнозируется равной  120,91 мм. Ошибка прогноза составляет не более 15,7% .

Приложения        

!!!! В отдельном файле “ Приложения”

Рекомендуемая литература

1.  Афифи А., Эйзен С. Статистичский анализ: Подход с использованим ЭВМ.–М.: Мир, 1982.– 488 с.

2.  Булига К.Б.,  Барановська Л.В. Практикум з теорії ймовірностей та математичної статистики: Навч. посіб.– К.: Європ. ун-т, 2000.-173 с.

3.  Боровиков В.П., Боровиков И.П. STATISTICA – Статистический анализ и обработка данных в среде Windows – Информационно-издательский дом “Филинъ”,1997.– 608 с.

4.  Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее
инженерные приложения. - М,: Наука, 1988. - 480 с

5.  Гмурман В.Е. Теория вероятностей и математическая статистика М.: Высшая школа, 1972 .- 368 с.

6.  Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике .- М.: Высшая школа, 1975- 333 с.

7.  Гнеденко В.В. Курс теории вероятностей. - М., Наука, 1969. - 400с.

8.  Гурский Е.И. Теория вероятностей с элементами математической статистики. - М.: Высшая школа, 1971. - 324 с.

9.  Дьяконов В. Mathcad 2001: учебный курс.–СПб.: Питер,2001. –624 с.

10. Калинина В.Н., Панкин В.Ф. Математическая статистика .-  М.: Высшая школа, 2001. - 336 с.

11. Карасев А.И. Теория вероятностей и математическая статистика. - М.: Статистика, 1979 - 279 с.

12. Макарова Н.В., Трофимец В.Я. Статистика в Excel: Учеб.пособие. – М.: Финансы и статистика,2002. – 368с.

13.    Манаков В.П., В.И. Ризун Теория вероятностей и математическая статистика: Учеб.пособие. – Алчевск: ДГМИ, 2000. -284 с.

14. Общая теория статистики: Учебник./под редакцией Спирина А.А., Башиной О.Э. –М.: Финансы и статистика, 1997.-296с.

15. Рыжов П.А. Математическая статистика в горном деле. - М.: Высшая школа, 1973. - 287 с.

16. Сборник задач по математике для втузов. Ч. 3. Теория вероятностей и математическая статистика: Учеб.пособие для втузов/Под редакцией А.В.Ефимова.– М.: Наука, 1990.– 428 с.

17.  Черняк О.І., Обушна О.М., Ставицький А.В. Теорія ймовірностей та математична статистика: Збірник задач: Навч. посіб.– К.: Т-во “Знання”, КОО, 2001.-199с.