Определение. Альтернативной (конкурирующей) называется гипотеза, конкурирующая с нулевой гипотезой в том смысле, что если нулевая гипотеза отвергается, то принимается альтернативная, которую обозначают символом Н1 .
Проверку статистических гипотез обычно осуществляют в следующем порядке:
А) Располагая выборочными данными х1, х2, …, хn и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу Н0, которую называют основной или нулевой, и конкурирующую гипотезу Н1 . Конкурирующая гипотеза представляет собой ту гипотезу, которая будет принята, если отвергнут основную гипотезу.
Б) Задаются вероятностью a, которую называют уровнем значимости ошибки первого рода. Поясним ее смысл. Решение о том, можно ли считать высказывание Н0 справедливым для генеральной совокупности, принимается по выборочным данным, т.е. по ограниченному ряду наблюдений, следовательно, это решение может быть ошибочным. При этом может иметь место ошибка двух родов: отвергают гипотезу Н0, или, иначе, принимают альтернативную гипотезу Н1, тогда как на самом деле гипотеза Н0 верна – это ошибка первого рода; принимают гипотезу Н0, тогда как на самом деле высказывание Н0 неверно, т.е. верной является гипотеза Н1 – это ошибка второго рода.
Значит, уровень значимости a - это вероятность ошибки первого рода, то есть вероятность того, что верная основная гипотеза будет отвергнута и принята ошибочная конкурирующая гипотеза.
В). Вводят статистический критерий проверки сформулированных гипотез, который представляет собой случайную величину, подчиняющуюся определенному заранее известному закону распределения, если верна основная гипотеза. По уровню значимости ошибки первого рода строят допустимую область (где принимается гипотеза Н0) и критическую область где отвергается гипотеза Н0 и принимается гипотеза Н1).
Г). По результатам выборки вычисляют наблюдаемое значение критерия и определяют область, в которую полученное значение критерия попадает. Если наблюдаемое значение критерия попало в критическую область, то гипотезу Н0 отвергают и принимают гипотезу Н1. Если наблюдаемое значение критерия попало в допустимую область, то говорят, что нет оснований отвергнуть гипотезу Н0 .
В математической статистике изучено множество различных гипотез, каждая из которых проверяется своим способом. Рассмотрим некоторые из них, наиболее часто встречаемых в горно-геологических статистических расчетах.
Имеем параметры выборок
по признаку Х: n1 – объем выборки; Sx2 – исправленная выборочная дисперсия;
по признаку У: n2 – объем выборки; Sу2 – исправленная выборочная дисперсия.
Пусть для определенности Sx2 > Sу2.
Требуется при заданном уровне значимости a сравнить дисперсии D(X) и D(Y) генеральных совокупностей.
Выдвинем основную и альтернативную гипотезы. Здесь рассмотрим два случая:
а) Н0: D(Х) = D(У) б) Н0: D(Х) = D(У)
Н1: D(Х) > D(У) Н1: D(Х) ¹ D(У)
Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия (отношение большей дисперсии к меньшей):
Этот критерий является случайной величиной, которая подчиняется закону распределения Фишера–Снедекора.
Критические области и точки зависят от выдвинутых альтернативных гипотез H1 .
а) Н1: D(Х) > D(У)
Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)
Fкр=F(a; k1; k2),
где a – заданный уровень значимости; k1 = n1 –1 - число степеней свободы большей исправленной дисперсии (Sx2); k2 = n2 –1 - число степеней свободы меньшей исправленной дисперсии (Sy2).
Если в результате сравнения окажется Fнабл < Fкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Fнабл > Fкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
б) Н1: D(Х) ¹ D(У)
Критическая область является двусторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)
Fкр=F(a/2; k1; k2),
где a – заданный уровень значимости; k1 = n1 –1 - число степеней свободы большей исправленной дисперсии (Sx2); k2 = n2 –1 - число степеней свободы меньшей исправленной дисперсии (Sy2).
Если в результате сравнения окажется Fнабл < Fкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Fнабл > Fкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
Имеем параметры выборок
по признаку Х: n1 – объем выборки; 
– выборочная средняя; Sx2 – исправленная выборочная дисперсия;
по признаку У: n2 – объем выборки; 
– выборочная средняя; Sу2 – исправленная выборочная дисперсия.
Требуется при заданном уровне значимости a сравнить математические ожидания М(Х) и М(У) генеральных совокупностей.
Перед тем, как решать поставленную задачу, нужно убедиться, что дисперсии сравниваемых совокупностей равны (см. п. 4.1). Далее решение осуществляется следующим образом: выдвигается основная и альтернативная гипотезы. Рассмотрим три случая:
а) Н0: M(Х) = M(У) б) Н0: M(Х) = M(У) в) Н0: M(Х) = M(У)
Н1: M(Х) > M(У) Н1: M(Х) < M(У) Н1: M(Х) ¹ M(У)
Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия
.
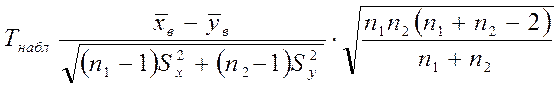Этот критерий является случайной величиной, которая подчиняется закону распределения Стьюдента с k = n1 + n2 – 2 степенями свободы.
Критические области и точки зависят от выдвинутых альтернативных гипотез H1 .
а) Н1: M(Х) > M(У)
Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.