Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 36

После заполнения 8–го столбца отмечаем, что  два последних элемента в этом столбце меньше пяти. Поскольку в   критерии Пирсона требуется, чтобы в каждом интервале было не меньше пяти единиц, то объединим частоты трех последних интервалов N_i^*  – для  8–го столбца;   N_i – для  3–го столбца.

11–ый столбец заполняем по формуле:  В_i =  .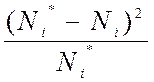

12–ый столбец – контрольный. Он вычисляется по формуле: V_i =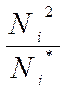 

Сделаем проверку: 49 + 7,4065 = 56,4065.    Верно.

          Запишем наблюдаемое значение критерия:  c²_набл = 7,4065.

Выберем уровень значимости ошибки  a=0,01.

Число степеней свободы равно k=l –3 , где  l  – число интервалов после объединения. В нашем случае число интервалов после объединения l=5.   Тогда число степеней свободы равно   k= 5 –3 = 2.  По таблице критических точек c²   находим   c²_кр(0,05; 2)= 6,0.

Сравниваем:         c²_набл > c²_кр .

Следовательно, необходимо отвергнуть гипотезу о нормальном законе распределения признака Х .

5.  Для признаков X и Y построим корреляционное поле в системе координат  ХОУ, используя исходную таблицу.

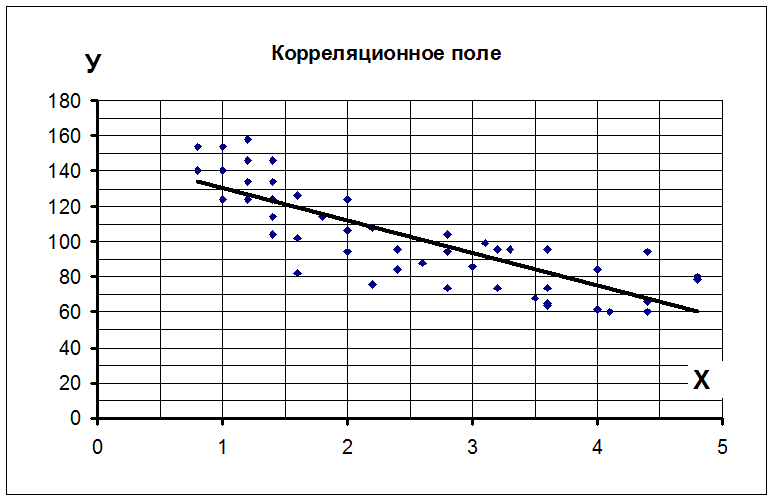
Корреляционное поле на данном рисунке характеризуется набором из 49 точек, причем можно заметить, что с увеличением  Х  признак У в среднем убывает.  Анализ полученного поля рассеяния позволяет предполагать наличие  прямой корреляционной зависимости  между признаками  Х  и  У.

  6.    Уравнение линейной регрессии имеет вид:  у = кх + b, где параметры   к  иb определяются по методу наименьших квадратов из условия минимального отклонения исходных точек корреляционного поля от прямой регрессии. Параметры   к  иb  вычисляются по формулам:

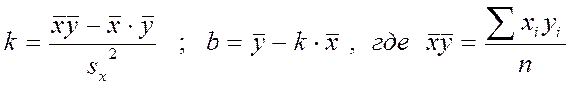
Для расчета этих величин заполним таблицу.