Учебно-справочное руководство по статистическим расчетам в изучении курса "Математическая статистика", страница 35

Б)  Для признака У  определим наибольшее и наименьшее значение признака:  У_min=60 ;        У_max=158  ;      объем выборки n = 49.

Найдем шаг разбиения  h = (У_max – У_min) / К.

В данном случае  h = (158-60 )/ 7 = 14.

Произведем группировку данных для признака У. Результаты группировки заносим в табл.2, которая представляет статистический ряд по признаку У.

    Таблица 2

Интервал	60 - 74	74 - 88	88-102	102-116	116-130	130-144	144-158
y  i	67	81	95	109	123	137	151
ni	10	9	10	6	5	4	5

 Проверка :  10+9+10+6+5+4+5=49.  Верно.

2.  А)  Построим полигон  и  гистограмму частот по признаку Х .

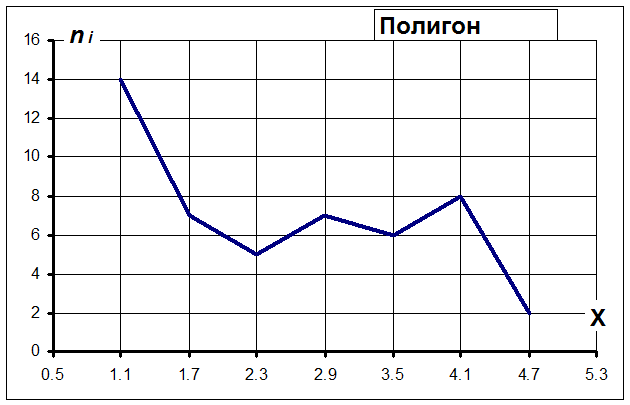
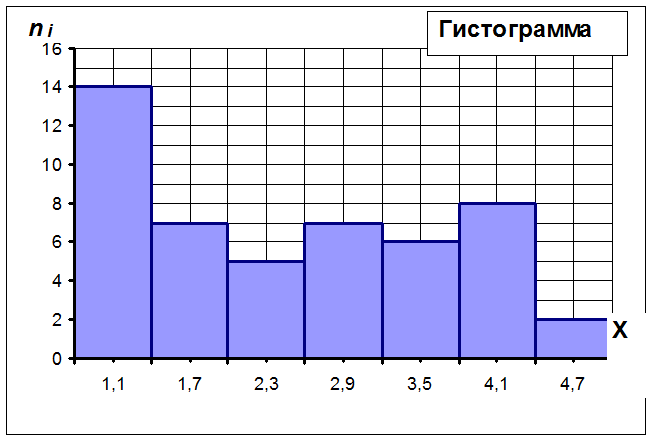
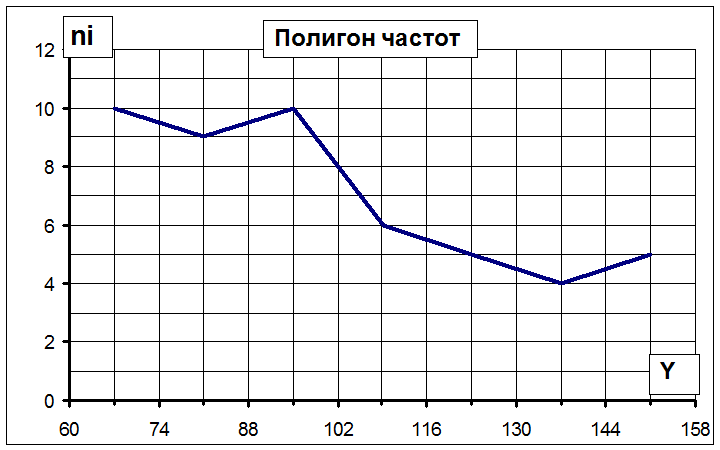Б)  Построим полигон  и гистограмму частот по признаку У

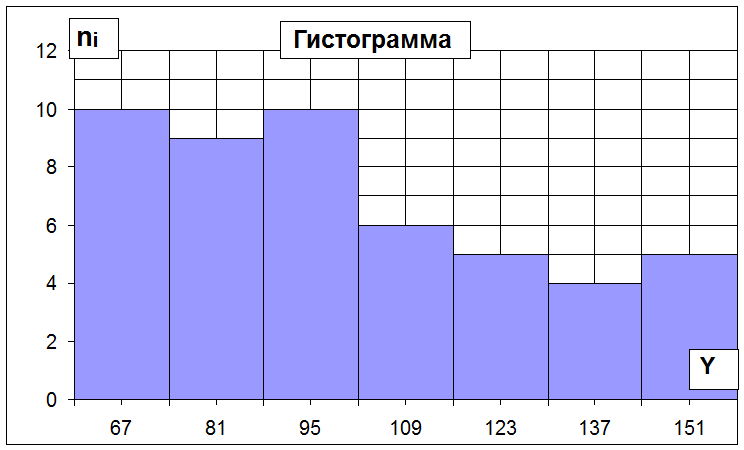
3.  А) Определим числовые характеристики выборки по признаку Х.

Используем метод “условного нуля ”. Выберем условный нуль из статистического ряда  признака : С = 2,9 .

Переходим к условным вариантам  по формуле: u_i = (x_i –C)/h, где h = 0,6.

 Далее заполняем специальную таблицу.

i	интервалы	xi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	0,8 -1,4	1.1	14	-3	-42	126	56
2	1,4 -2	1.7	7	-2	-14	28	7
3	2 -2,6	2.3	5	-1	-5	5	0
4	2,6 - 3,2	2.9	7	0	0	0	7
5	3,2 - 3,6	3.5	6	1	6	6	24
6	3,6 - 4,4	4.1	8	2	16	32	72
7	4,4 - 5	4.7	2	3	6	18	32
итого			49		-33	215	198

Для проверки правильности вычислений используем тождество:

           ån_i(u_i+1)² = ån_iu_i² + 2ån_iu_i + n

  Получим:    198 = 215 + 2·(–33) + 49

                         198 = 198    – верно.

Из таблицы находим условные моменты:

М₁ = ån_iu_i / n = -33/49 = –0,6735

М₂ = ån_iu_i² / n = 198/49 = 4,3878;

Выборочная средняя равна:  = М₁·h + C =  –0,6735×0,6 + 2,9 = 2,50

Выборочная дисперсия равна:

D_в = [M₂  - (M₁)²]·h²=  [4,3878 – (-0,6735)²]·0,6² = 1,4163         

Выборочное среднее квадратическое отклонение равно

 1,19

Вычислим исправленную выборочную дисперсию

S ² = 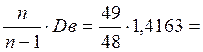 1,4458

Вычислим исправленное выборочное среднее квадратическое отклонение:

 1,2024.  Обозначим результат  S _x = 1,2 .  

Полученные результаты позволяют сделать следующие выводы.

Средняя скорость подвигания очистного забоя по выборке равна 2,5 м/сут. Средний разброс скорости подвигания очистного забоя вокруг среднего по выборке равен 1,2 м/сут.

 Б)  Аналогично  определяем  числовые характеристики выборки по признаку У .   Выберем условный нуль С = 109 ; h = 14.

i	интервалы	уi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	60 - 74	67	10	-3	-30	90	40
2	74 - 88	81	9	-2	-18	36	9
3	88-102	95	10	-1	-10	10	0
4	102-116	109	6	0	0	0	6
5	116-130	123	5	1	5	5	20
6	130-144	137	4	2	8	16	36
7	144-158	151	5	3	15	45	80
итого			49		-30	202	191

Проверка:        191 = 202 + 2·(–30) + 49  –  верно.

Из таблицы находим условные моменты:

М₁ =  -30/49 = –0,6122;

М₂ = 202/49 = 4,1224;

Выборочная средняя равна:  =  –0,6122×14 + 109 = 100,43

Выборочная дисперсия равна:

D_в = [M₂  - (M₁)²]·h²=  [4,1224 – (-0,6122)²]·14² = 734,5306           

Выборочное среднее квадратическое отклонение равно

=27,1022.

S ² = 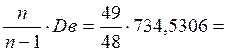 749,8333

27,383 . Обозначим результат  S _у = 27,383 .

Полученные результаты позволяют сделать следующие выводы.

Средняя величина опускания кровли по выборке равна 100,43 мм. Средний разброс величины опускания кровли  вокруг среднего по выборке равен 27,383мм.

4.  Проверим гипотезу о нормальном распределении признака Х.  Выдвинем гипотезы

     Н₀:  Признак Х подчиняется нормальному закону распределения      

     Н₁:  Признак Х не подчиняется нормальному закону распределения

Для проверки гипотез используем критерий Пирсона. В качестве исходных данных берем интервальный ряд признака Х, полученный в п1. решения данной задачи и характеристики выборки признака Х, найденные в п.:

    =2,5;    S_x =1,2

Далее  заполним таблицу по формулам:  

z _i = (х _i – )/S_х ;   z _i+1 = (х _i+1 – )/S_х .

Теоретические частоты найдем по формуле:  n_i^*=n×[Ф(z_i+1) – Ф(z_i)], где  функция Ф(z) вычисляется по таблице.