- закройте рисунок и вернитесь в Word.
4. Найдите в полученной диаграмме (она представлена на рис. 5) группы провайдеров в нижней левой части, в нижней правой части и вверху.
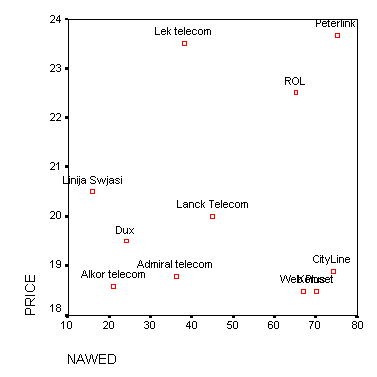
Рис. 5. Диаграмма рассеяния для Интернет-провайдеров
Поиск их формальными методами и есть сущность кластерного анализа. Таким образом, программа ищет такие группы элементов исследования, внутри которых эти элементы схожи, а между группами различаются в большей степени.
Ситуации, подобные приведенной в примере, когда группы видны «невооруженным глазом», достаточно редки. Чаще границы кластеров размыты. Количество переменных обычно значительно превышает 2, что не позволяет строить наглядные диаграммы. Поэтому приходится применять математические формулы.
Эти формулы основаны на оценке расстояния между точками, соответствующими элементам исследования. В качестве меры расстояния d(A,В) между точками А и В чаще всего применяется евклидово расстояние:
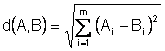 ,
,
где Ai и Bi – i-е координаты точек А и В соответственно, m – число координат.
К другим мерам расстояния между элементами исследования относятся:
- квадрат евклидова расстояния между точками;
- корреляция между наборами наблюдений за парой элементов исследования.
Все вышеприведенные меры имеют следующий недостаток: расстояние, вычисляемое по ним, зависит от шкалы измерения переменных. Например, если бы цена измерялась не в рублях, а в условных единицах, расстояния были бы другими. Для решения данной проблемы используют так называемые z-шкалы, в которых из значений переменных вычитают их среднее значение и делят на стандартное отклонение. Иногда путем линейных преобразований добиваются того, чтобы все измеренные значения находились в диапазоне от -1 до 1. Существуют и другие методы стандартизации значений переменных различной природы.
В иерархических методах кластеризации каждый элемент исследования образовывает сначала свой отдельный кластер. На первом шаге два самых близкорасположенных кластера, содержащих пока по одному элементу, объединяются в один кластер. Далее процесс слияния кластеров продолжается до тех пор, пока не получится один кластер. Каждый факт слияния характеризуется некоторым значением расстояния, при котором оно произошло. Если установлено правило Nearest neighbor (ближайший сосед; простая кластеризация), то будут получаться кластеры в виде цепочек. Правило Furthest neighbor (самый дальний сосед; полная кластеризация) дает компактные кластеры, а правило Between groups linkage (межгрупповая связь; кластеризация по среднему расстоянию) занимает промежуточное положение между первыми двумя. Правда, следует отметить, что, как и всегда, когда вычисления основаны на большом числе данных, результаты, полученные с помощью последнего правила, менее чувствительны к случайным ошибкам при сборе данных.
Для получения кластеров из точек, изображенных на рис.5, выполните следующие действия.
1. Откройте файл Internet.sav.
2. Выберите Analyze à Classify à Hierarchical cluster… (Анализировать à Классифицировать à Иерархический кластерный [анализ]).
3. В появившемся окне выберите переменные Price и Nawed (см. табл. П.5) и выберите их для анализа, нажав кнопку со стрелкой. Выбранные переменные должны попасть в окно, расположенное правее и имеющее название Variable(s) (переменные).
4. Текстовую переменную Company аналогичным образом переместите в поле Label cases by: (пометить наблюдения как).
5. Проверьте установку основных режимов расчета.
В рамке Cluster с помощью радиокнопок можно выбрать, что группировать: наблюдения (кнопка Cases) или переменные (кнопка Variables). В рамке Display (отображать) можно снять флажок Statistics (статистики), чтобы не перегружать окно результатов, если от анализа потребуется только график. Если же не требуется вывод графиков, то снимается флажок Plots.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.