Управление продуктом: Методические указания по выполнению курсового проекта и проведения практических занятий, страница 19

на координатной плоскости X, Y. Здесь X_Ni – нормированная величина, характеризующая объем продаж i-го товара[10]:

  ,    ,  ,

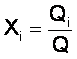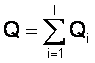где Q – общий объем сбыта анализируемых товаров предприятия за все периоды, тыс. руб.; I – количество товаров (в курсовом проекте 12); Y_Ni – нормированная величина, характеризующая изменение (рост, если величина положительная или снижение, если отрицательная) объема продаж i-го товара.

Величины Х_max и Y_max определяются по формулам:

  ;    .

Объясните, зачем в формуле для Y_max используется абсолютная величина. Эта задача упростится после того, как Вы выполните вычисления по вышеприведенным формулам.

Построение матрицы предлагается выполнить средствами MS Excel.

1.  Начинать следует с копирования исходных данных Вашего варианта на лист электронной таблицы. Лучше сразу снабдить таблицу обозначениями строк и столбцов аналогично табл. 1.

2.  Для определения применимости предлагаемого метода построения матрицы делается оценка разброса суммарных объемов выпуска по всем периодам для различных товаров.

Если величина вариации суммарных объемов выпуска по всем периодам для различных товаров превышает 0,5, построение матрицы возможно. В противном случае анализ нецелесообразен, так как все товары имеют практически одинаковый объем выпуска.

Проверка применимости метода для анализа изменений объемов продаж производится после определения величины наклона линий тренда.

3.  Рассчитайте итоги по строкам (Q_i) и столбцам (Q_t) таблицы с помощью формул Excel. Эти итоги приведены в табл.1.

4.  Для столбца итогов Q_i (см. табл. 1) определите максимум, используя функцию МАКС(БлокЯчеек).

5.  В новом столбце справа от таблицы исходных данных, озаглавленном Объем, получите значения итогов Q_i, деленные на полученный максимум. Это значения .

6.  Определите значения наклона объемов продаж по каждому товару. Для этого в новом столбце, озаглавленном Наклон (правее существующих) рассчитайте значение формулы

=НАКЛОН(ЗначенияФункции;ЗначенияАргумента).

Для первого товара в качестве ЗначенийФункции укажите блок ячеек, содержащий его объемы продаж (в примере это 37,6; 36,0; 36,2; 32,1; 32,4; 28,1) а в качестве ЗначенийАргумента – блок ячеек, содержащий номера периодов (значения 1; 2; 3; 4; 5; 6). Для последующих товаров ЗначенияАргумента остаются теми же, а ЗначенияФункции берутся из строки, соответствующей данному товару.

7.  В новом столбце, озаглавленном Модуль, с помощью функции ABS(Ячейка) определите абсолютную величину каждого из полученных значений наклона.

8.  Найдите максимальное значение столбца Модуль, аналогично п. 4.

9.  В последнем столбце, имеющем название Рост, рассчитайте частное от деления значений столбца Наклон на максимальное значение, полученное в п. 8. Это значения .

10.  Перенесите полученные значения в отдельную таблицу (табл. Таблица 5) для построения диаграммы.

11.  Постройте по полученной таблице точечную диаграмму. Ее пример для исходных данных табл. Таблица 2 дан на рис. Рис. 3. Этот рисунок и представляет собой модифицированную матрицу БКГ.

На основании матрицы БКГ можно разделить товары ассортимента на четыре группы: «дойные коровы» с малым ростом, но большой долей в объеме продаж; имеющие большую долю в объеме продаж и быстрорастущие «звезды»; «собаки», рост которых мал при малых объемах, и «дикие кошки», имеющие малый объем продаж, но быстрый рост[11]. Их обозначения в табл. Таблица 5: С – собака, К – дойная корова, З – звезда, ? – дикие кошки (их называют иногда «знаками вопроса»).