Задача 12. Найдите все комплексные числа z, для которых z4 = 1; z4 = –1.
Если z4 = 1, то z2 = ±1. Далее, если z2 = 1, то z = ±1. Если же z2 = –1, то z = ±i. Так мы нашли четыре решения первого уравнения.
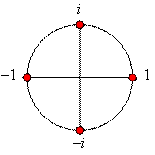
Пусть теперь z4
= –1. Тогда z2 = ± i.
Далее, если z2 = i,
то 
(можно найти этот результат
геометрическим рассуждением, а можно и алгебраически). Если же z2 = – i,
то 
. Так мы нашли четыре решения второго
уравнения.
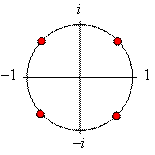
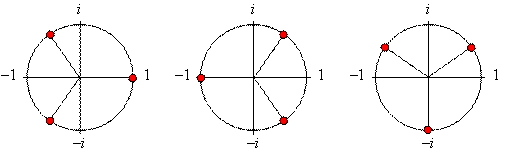
Задача 13. Найдите все комплексные числа z, для которых z3 = 1, z3 = –1, z3 = i.
Задача 14. Найдите все комплексные числа z, для которых z2 = 1 + i .
Решение 1. Решение
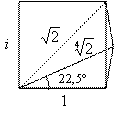
этого уравнения нам по сути дела уже известно. Его модуль равен 
, а его аргумент равен 22,5° = 
. Тем самым z
= 
. Правда, мы пока не знаем, чему
здесь равны значения синуса и косинуса. Но мы это сейчас узнаем!
Решение 2. Будем искать z в виде z = x + iy. Тогда z2 = (x + iy)2 = (x2 – y2) + 2ixy = 1 + i. Приравнивая порознь действительные и мнимые части, получаем систему:
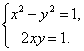
Отсюда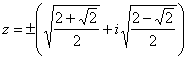 
.
Следствие. Тем
самым 
, 
.
Задача 15. Найдите все комплексные числа z, для которых z5 = 1.
Один корень этого уравнения мы
знаем: это z = 1. Деля в столбик z5 – 1 на z –
1, приводим уравнение к виду (z – 1)(z4 + z3
+ z2 + z
+ 1) = 0. Как нам справиться со второй скобкой? Разделив её на z2, получим уравнение 
.
Сделаем замену 
. Вычислим 
. Тем самым имеем квадратное
уравнение w2 + w
– 1 = 0. Отсюда 
. Далее, из уравнения z2 – wz + 1 = 0
получаем 
. Отсюда
,
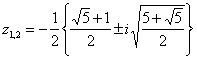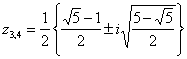, z5
= 1.
Задача 16. Известно, что z + 1/z = 2cos l°. Найдите z60 + 1/z60.
Поскольку z + 1/z — действительное число, тем самым z лежит на единичной окружности. Удобно ввести обозначение Iα для единичного отрезка, повёрнутого на угол α. Но тогда z = I1°. Тем самым z60 = I60°. Поэтому z60 + 1/z60 = 2cos60° = 1.
Задача 17. Выведите формулы, выражающие cos(α + β) и sin(α + β) через cosα, sinα, cosβ, sinβ.
Представим соотношение Iα · Iβ = Iα+β в тригонометрическом виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.