Программа профильной лаборатории «Учебное исследование в математике», страница 17

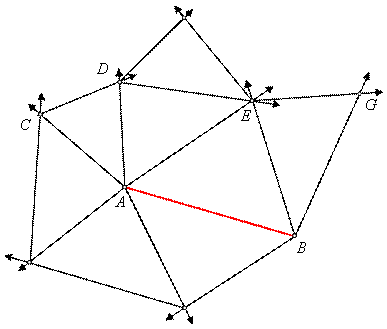
Именно для решения такого рода задач Вессель и придумал своё исчисление направленных отрезков. Кстати сказать, статья, в которой он это исчисление описал — это его единственная математическая работа за всю жизнь.

Как складывать и вычитать направленные отрезки, интуитивно понятно: как последовательные перемещения, «векторы». Но для полноты исчисления нужно также научиться умножать направленные отрезки и делить. При этом надо предупредить, что умножение направленных отрезков по Веселю будет отличаться от умножения векторов, если кто-то о таком умножении уже знает. Скалярное произведение двух векторов даёт число — а наше произведение направленных отрезков будет направленным отрезком.

Между прочим, с подобной ситуацией мы уже сталкивались раньше. Мы могли считать, что произведение двух отрезков (не направленных, а обычных отрезков) равно площади прямоугольника, построенного на этих отрезках, как на сторонах. Но можно определить произведение двух отрезков и иначе. Надо взять единичную мерку (например, 1 см), выразить длину обоих отрезков через эту мерку (например, 4 см и 6 см), перемножить длины (4 · 6 = 24) и построить отрезок полученной длины 24 см. Конечно, такой результат будет зависеть от выбора единичной мерки. Но когда мы её выберем, такое перемножение станет возможным.

Вессель в своих построениях опирался на аналогичную идею. Пусть мы хотим перемножить два направленных отрезка  и , получив в результате некий отрезок . С этой целью зададим на плоскости направленный единичный отрезок , и введём следующее правило: для всякого отрезка  выполняется соотношение . Запишем соотношение  в виде , а затем перепишем его в виде пропорции .

Пока что наши действия были формальными, но теперь мы наполним их содержанием, сказав:  должен так же получаться из , как  получается из . Но как  получается из ? Во-первых, нужно умножить отрезок  на некоторое положительное число, чтобы он растянулся (или сжался) до длины , а во-вторых, нужно повернуть результат на некоторый угол α, чтобы совместить его с . Стало быть, чтобы из  получить , надо  умножить на то же самое положительное число, растянув (сжав) его во столько же раз, а затем надо повернуть результат на тот же самый угол α.

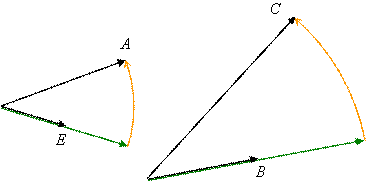
Удобно видеть на этой картинке два подобных одинаково ориентированных треугольника:

Тема 3. Комплексные числа как отношения направленных отрезков

Задача 1. На плоскости задан своими декартовыми координатами единичный отрезок  = (1, 0). Также даны отрезки  = (1, 1),  = (–4, 2). Постройте отрезки , , , , , , , .