Программа профильной лаборатории «Учебное исследование в математике», страница 18

При умножении и делении будем пользоваться тем, что в данном случае  относится к , как диагональ квадрата к его стороне (и по длине, и по направлению тоже).

При возведении в степень естественно также задаться вопросом, где будут находиться концы отрезков, выражающих дробные и отрицательные степени.

Задача 2. Для данного направленного отрезка  ≠ 0 найдите обратный ему направленный отрезок  (иначе говоря, найдите такой отрезок , для которого ).

Задача 3. Найдите два направленных отрезка, сумма и произведение которых рав­ны .

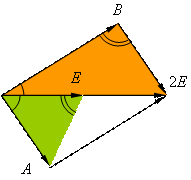
Решение 1. Сумма направленных отрезков определяется по правилу параллелограмма. Уравнение для произведения мы перепишем в виде , откуда . Поэтому закрашенные на рисунке треугольники должны быть подобными. Из равенства углов, отмеченных одной дугой, следует, что рассматриваемый параллелограмм является ромбом; но диагонали ромба перпендикулярны, и поэтому углы, отмеченные двумя дугами, являются прямыми. Следовательно, искомый параллелограмм является квадратом.

Решение 2. Положим , , чтобы сразу же было . Отсюда получаем . Но должно быть , откуда , что можно представить в виде пропорции . Стало быть,  так получается из , как  получается из . Во-первых, поскольку  и  имеют единичную длину, тем самым и  имеет единичную длину. Во-вторых,  получается из  поворотом на ±180° , поэтому  получается из  поворотом на ±90°. Но ведь  — это ; вот мы и получили мнимую единицу!

Тема 4. Отображения плоскости

До сих пор мы вели речь о направленных отрезках; теперь мы постепенно переходим к разговору о комплексных числах. Это означает, что каждой точке «комплексной плоскости» мы поставим в соответствие «комплексное число», которое выражает отношение направленного отрезка, соединяющего начало координат с этой точкой, к единичному направленному отрезку. При этом мы будем помнить, что число — это всё-таки не точка, а отношение направленных отрезков. Хотя точку тоже можно отождествлять с числом, а число можно представлять точкой. Но перемножаем мы всё-таки не точки, и даже не отрезки, — а отношения отрезков.

Задача 4. Точка z обходит окружность радиуса 1 с центром в начале координат против часовой стрелки. Нарисуйте траекторию точки (a) 2z – 1; (б) z² ; (в) z³ ; (г) 1/z; (д) z + l/z.

Задача 5. Точка z пробегает прямую, проходящую через конец единичного отрезка  перпендикулярно к нему. Как при этом будет двигаться точка 1/z?