Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 9

Как вы знаете, кроме соседних есть еще и несоседние вершины. У многоугольника они получили название противолежащих (противопо-ложных).

Отрезки, соединяющие противолежащие вершины называются диагоналями.

Как и вершины, несоседние стороны называются противолежащими (противоположными).

А2

У многоугольника А₁А₂…А_nА₁ (рис. 1.13) вершины А₁ и А₂ – соседние, А₁ и А₃ – противолежащие, , отрезок А₁А₃ – диагональ, стороны А₁А₂ и А₁А_n - соседние, стороны А₂А₃ и А₁А_n – противолежащие.

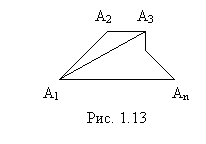§ 5.3 Сумма углов многоугольника.

Стороны и углы многоугольника обладают количественными характеристиками, - длиной и градусной мерой соответственно. Мы знаем, что ломаная в общем случае может иметь произвольные длины звеньев и произвольные величины углов. А произвольны ли эти параметры для многоугольника?

Ответ отрицательный даже для простейшего многоугольника – треугольника. Как вы знаете, не из любых трех отрезков составляется треугольник, и сумма углов всех треугольников одинакова. Таким образом замкнутость ломаной – это очень сильное ограничение.

Вопрос для общеклассной дискуссии: Какому условию должны удовлетворять отрезки, чтобы по ним можно было построить многоугольник?

5.3.1 Сумма углов четырехугольника.

Проблема: Мы имеем удивительный факт: сумма углов у всех треугольников одна и та же. Имеет ли место этот факт для других многоугольников?

Рассмотрим аналогичный треугольнику четырехугольник (рис.1.14).

Если в данном четырехугольнике провести диагональ (рис.1.15), то видно, что сумма углов четырехугольника равна сумме углов двух треугольников.

Таким образом, сумма углов четырехугольника, аналогичного треугольнику, не произвольна, а всегда одна и та же – 360^о.

Вопрос для общеклассной дискуссии: Опишите способ, при помощи которого удалось найти сумму углов четырехугольника. За счет чего оказалось возможным найти сумму углов четырехугольника на рис.1.14?

Задание: Приведите примеры четырехугольников, имеющих угол, измеряемая величина которого не равна сумме величин соответствующих углов треугольников, образованных диагональю.

Рассмотрим следующий рисунок (рис.1.16).

Чем фигура на рис.1.16 отличается от четырехугольника на рис.1.14?

У четырехугольника на рис.1.14 поперечины всех углов лежат в многоугольной области, а у четырехугольника на рис.1.16 – нет (рис.1.17).

Из-за того, что у четырехугольника на рис.1.16 поперечина угла С лежит вне многоугольной области, описанный выше способ нахождения суммы углов четырехугольника на данной фигуре не работает.