Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 15

2.4.3 Квадрат

С квадратом вы знакомы уже давно и поэтому, возможно, считаете, что знаете о нем все. Здесь вам предоставляется возможность проверить свои знания.

Квадратом называется ромб, у которого все углы прямые (рис. 2.16).

Задание: Сформулируйте все свойства квадрата.

Задание: Придумайте признаки квадрата.

Глава 3. Площадь

§ 3.1 Понятие площади.

Вам понятен смысл слов «Отрезок АВ равен отрезку CD» или «Треугольник АВС равен треугольнику А₁В₁С₁». Для некоторых фигур вы даже знаете, как определить, равны они или нет.

А если фигуры не равны, то в каком отношении они находятся? Может ли одна фигура быть больше или меньше другой? И вообще, любые две фигуры можно сравнить между собой? Предлагаем эти вопросы для обсуждения в классе.

Задание: Сравнить фигуры 3.1.а) и 3.1.б).

По какому признаку вы сравнили эти фигуры?

Мы предполагаем, что вы сравнили эти фигуры по площади их многоугольных областей. Видно, что площадь той части плоскости, которую ограничивает фигура 3.1.б), больше площади части плоскости, которую ограничивает фигура 3.1.а).

Является ли площадь многоугольной области величиной? Существует ли способ измерения площади многоугольной области?

В дальнейшем для краткости речи площадь многоугольной области будем называть площадью многоугольника.

Задание: Вспомнить, как измеряются величины. Как измеряются площади?

Итак, для измерения площади конкретной фигуры можно взять за мерку (единицу измерения) любую другую фигуру из соображений удобства. При выборе мерки важную роль играет ее форма. Для одних фигур удобно выбрать мерку одной формы, а для других – другой формы (может быть даже той же площади).

Выбор мерки из соображений удобства не всегда эффективен. Например, в общем случае мы не сможем сравнить площади фигур, измеренные разными мерками. Так же мы не сможем пользоваться результатами измерений других людей, потому что не будем знать, какую мерку посчитали удобным взять они.

Чтобы можно было сравнивать результаты измерений или использовать чужие, нужно договориться о универсальной мерке, о форме универсальной мерки.

Вопрос для общеклассной дискуссии: Что бы вы предложили в качестве универсальной мерки?

Универсальной меркой для измерения площади является квадрат.

Аксиома. Квадрат имеет площадь.

Чтобы найти площадь, в фигуру укладывают квадрат, выбранный за мерку, и его части, которые имеют площадь.

Число, которое показывает, сколько раз квадрат и его части укладываются в фигуру, называется численным значением площади.

Численное значение площади зависит от величины квадрата, выбранного за мерку. Чем больше величина квадрата, тем меньше численное значение площади фигуры (рис.3.2).

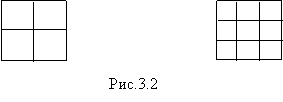Хотя численное значение площади может меняться, сама площадь фигуры есть постоянная величина.

Задание: Найдите площади квадратов на рис.3.2. Запишите численные значения площадей этих квадратов.

Очевидно, что численное значение площади квадрата, выбранного за мерку, равно 1. Поэтому квадрат (универсальная мерка) называется единичным квадратом.

Непосредственное по определению измерение площади фигуры не удобно. Для многих фигур оно связано с дроблением мерки, которое может продолжаться бесконечно, трансформацией фигуры. В то же время фигура может быть задана своими линейными характеристиками (длинами сторон, высот, биссектрис, медиан, радиусов вписанных и описанных окружностей, величин углов и т. д.).