Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 16

Поставим задачу опосредованного нахождения, то есть вычисления площади многоугольника по известным линейным элементам. Формулы, показывающие связи площади фигуры и значения ее линейных элементов, будем называть формулами вычисления площади.

§ 3.2 Площадь прямоугольника.

Замена измерения вычислением требует согласования и установления связи линейных мер и мер площади и, прежде всего, установления связи стороны единичного квадрата и его площади.

3.2.1 Площадь единичного квадрата.

Пусть сторона единичного квадрата равна единице измерения е. Так как мы взяли единичный квадрат, то численное значение его площади равно 1. А чему равна его площадь как величина?

Вопрос для общеклассной дискуссии: Существуют ли способы вычисления площади единичного квадрата как величины?

Договоримся площадь единичного квадрата со стороной е обозначать е².

3.2.2 Площадь прямоугольника.

Вычислим площадь прямоугольника. Начнем с примера.

Найдем S - площадь прямоугольника ABCD со сторонами АВ=е и ВС=а.

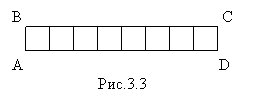Измерение площади прямоугольника АВСD единичным квадратом сводится к измерению сторон прямоугольника меркой е (рис.3.3): S/е²=а/е. Тогда площадь данного прямоугольника S=(а/е)е².

Если е численно принять за 1, то S=а.

Далее мы во всех формулах вычисления площади будем е численно принимать за 1.

Теперь мы можем найти площадь любого прямоугольника (рис.3.4).

Задание: Найти площадь прямоугольника ABCD (рис.3.4), если известно, что АВ=а и ВС=b.

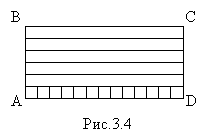3.2.3 Площадь прямоугольного треугольника.

Какие новые возможности дает знание формулы площади прямоугольника?

Разобьем прямоугольник ABCD диагональю на два равных прямоугольных треугольника (рис.3.5). Можно ли найти их площади, зная площадь прямоугольника?

Вы наверно предположили, что площадь одного треугольника равна половине площади прямоугольника. Но, чтобы сделать такой вывод, необходимо знать, что:

1)  если треугольники равны, то и их площади равны;

2)  площадь прямоугольника равна сумме площадей треугольников.

Вы убедились, что наличие свойств 1) и 2) облегчит вычисление площадей некоторых фигур. Но ранее не было сказано, что площадь многоугольника обладает свойствами, подобными 1) и 2).

Естественно, если мы применим процесс измерения одной и той же меркой к равным фигурам, то получим одинаковые численные значения площадей. Следовательно, и площади как величины равных фигур будут равны.

Договоримся, что если фигура разбита на части, имеющие площади, то площадь фигуры равна сумме площадей ее частей.

Это не очень очевидное свойство. В случае измерения фигуры и ее частей мы имеем разные процессы измерения. Зачастую измерение фигуры может быть выполнено проще, чем измерение ее частей.

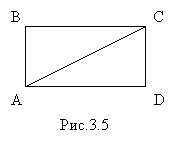
Вернемся к прямоугольным треугольникам (рис.3.5).

Используя свойства площади, получаем, что площадь прямоугольного треугольника равна половине площади прямоугольника, построенного на катетах треугольника.

Если а, b – длины катетов прямоугольного треугольника, то его площадь выражается формулой

S=ab/2.

Задание: Используя формулу площади прямоугольника, вывести формулу для вычисления площади ромба.