Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 22

«Углом выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине» [17, c.203].

«Рассмотрим выпуклый n–угольник, изображенный на рисунке 155.а. Углы А_nА₁А₂, А₁А₂А₃, ..., А_n-1А_nА₁ называются углами этого многоугольника.

…» [3, c.95].

Если отделить понятие внутреннего угла многоугольника от понятия линейного угла, то способ триангуляции позволит находить сумму углов произвольного простого многоугольника.

«Внутренним углом многоугольника при данной вершине называется плоский угол при этой вершине, который в достаточно малой окрестности вершины содержит часть многоугольной области (рис.1.21).

…» [c.24].

Следует отметить, что мы не первые, кто помещает в учебник обобщенную до произвольного простого многоугольника теорему о сумме углов треугольника.

«Зная сумму углов треугольника, легко получить формулу для суммы углов любого n-угольника.

Рассмотрим, например, выпуклый семиугольник (рис.126). Соединим какую-либо его вершину диагоналями со всеми остальными вершинами.

Таким же образом можно поступить и с любым выпуклым n-угольником. Сумма его углов равна (n-2)*180^о.

Невыпуклый многоугольник нельзя так просто разбить на треугольники. Тем не менее, формула для суммы его углов остается прежней. (На рисунке 127 показан пример разбиения невыпуклого семиугольника.)» [21, c.114].

8. Обобщая теорему о сумме углов треугольника, мы столкнулись с проблемой выбора способа введения понятия выпуклости. Было рассмотрено два варианта:

1)  ввести понятие выпуклости через прямые, содержащие стороны многоугольника (по традиции);

2)  ввести понятие выпуклости через многоугольную область и поперечины углов многоугольника.

Текст учебника позволяет воспользоваться любым из этих способов.

«Чем фигура на рис.4.8 отличается от четырехугольника на рис.4.7?

Четырехугольник на рис.4.7 полностью лежит в одной полуплоскости относительно любой прямой, содержащей его сторону, а четырехугольник на рис.4.8 – нет.»

«Чем фигура на рис.4.8 отличается от четырехугольника на рис.4.7?

У четырехугольника на рис.4.7 поперечины всех углов лежат в многоугольной области, а у четырехугольника на рис.4.8 – нет.»

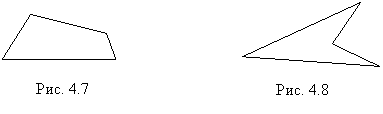В обоих случаях мы по-разному отвечаем на один и тот же вопрос. Но при решении проблемы углов многоугольника второй ответ выглядит более естественным, чем первый.

Таким образом, само содержание учебника определило способ введения понятия выпуклости многоугольника.

«Многоугольник называется выпуклым, если поперечина любого его угла лежит в многоугольной области, ограниченной этим многоугольником» [c.22].

§ 4.3 Объяснительная записка к главе «Четырехугольники».

1. Чтобы следовать принятому принципу изложения материала вокруг явно выделенных вопросов и проблем, авторы должны были определить, решением какой проблемы могут явиться классические четырехугольники: трапеция, параллелограмм, прямоугольник, ромб и квадрат.