Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 25

Чтобы всякий раз, когда нужно измерить площадь, не приходилось решать проблему определения площади мерки, математики решили стандартизировать мерку. В качестве мерки выбрана фигура максимально правильной формы (квадрат), наличие площади которой взято за аксиому.

Несмотря на стандартизацию мерки, отказываться от квадрируемых фигур произвольной формы не стоит. Квадрируемые фигуры произвольной формы могут быть использованы как посредники для измерения площади. Фактически речь идет о проблеме, которую мы пока не рассматриваем в учебнике, но которая может быть рассмотрена на факультативных занятиях, - классической проблеме равносоставленности.

Проблема равносоставленности представляется задачами на разрезание, в которых одну фигуру надо разрезать на такие части, из которых можно составить другую наперед заданную фигуру.

Практическое значение равносоставленных фигур заключается в их равновеликости. Так, не имея возможности измерить площадь фигуры, данную фигуру можно заменить на равносоставленную, площадь которой  не составит труда найти.

Глава 5. Методические указания.

§ 5.1 Краткие комментарии к тексту первой, второй и третьей глав учебника

1.  Первый урок рекомендуем начинать с повторения материала из курса геометрии за 7 класс. Следует вспомнить, что изучает наука геометрия. Желательно вспомнить все изученные геометрические фигуры и их определения. Следует повторить типы геометрических фигур – основные и составные, и разделить изученные фигуры по типам. Желательно вспомнить, в каких отношениях могут находиться разные геометрические фигуры. Например, прямые могут находиться в отношении пересечения, параллельности или перпендикулярности, точка может находиться в отношении принадлежности отрезку.

2. 

Количество начал и концов (подробно) у фигуры из двух отрезков, имеющей два конца, зависит от того, как получена фигура. Она может иметь два начала (рис.5.1.а); может иметь два конца (рис.5.1.б); может иметь одно начало и один конец (рис.5.1.в, г).
         Мы рекомендуем рассуждение о количестве начал и концов фигуры из двух отрезков сделать в форме доклада, подготовленного учениками.

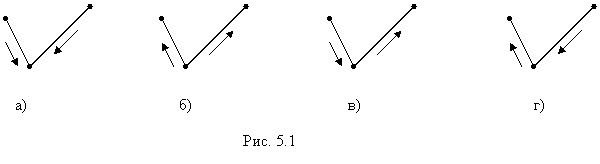3.  В учебнике способом опознавания ломаной является подсчет начал и концов фигуры, состоящей из отрезков. На практике этот способ не всегда удобен, потому что у некоторых фигур довольно трудно найти начала и концы.
         Мы предлагаем акцентировать внимание учеников на том, что фигура является ломаной, если ее можно нарисовать, не отрывая карандаша от бумаги и не проводя ни по одной линии дважды.

4.  При рассмотрении соотношений звеньев ломаной мы рекомендуем перебрать все возможные случаи пересечения не соседних звеньев: пересечение в вершине, пересечение не в вершине, прохождение звена через вершину. На доску надо заносить соответствующие рисунки.
          Типология самопересечений ломаной потребуется в параграфе «Многоугольник».

5.  Первое и последнее звенья замкнутой ломаной соединены опосредованно через другие звенья, поэтому по общему определению соседних звеньев незамкнутой ломаной не являются соседними. Однако на замкнутой ломаной невозможно указать, какое звено является первым, а какое - последним: любые два звена с общей вершиной можно считать ими. По этой причине первое и последнее звенья замкнутой ломаной удобнее считать соседними.

6.  В соотношениях звеньев не рассматривается случай наложения звеньев. Мы предлагаем рассмотреть его на факультативных занятиях.

7.  Прежде чем переходить к изучению многоугольника, мы рекомендуем учителю исследовать проблему соотношений числа звеньев и числа вершин ломаной. В учебнике приведены не все возможные соотношения. Например, мы не рассматривали численные соотношения звеньев и вершин ломаных с самопересечением в вершинах.