Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 10

Дадим название тем четырехугольникам, на которых работает способ.

Четырехугольник называется выпуклым, если поперечина любого его угла лежит в многоугольной области, ограниченной этим четырехугольником.

Итак, все выпуклые четырехугольники имеют одну и ту же сумму углов, и она равна 360^о.

5.3.2 Сумма углов выпуклого многоугольника.

Очевидно, что описанный способ нахождения суммы углов работает не только на четырехугольниках, но и на всех многоугольниках, у которых поперечины углов лежат в многоугольных областях.

Многоугольник называется выпуклым, если поперечина любого его угла лежит в многоугольной области, ограниченной этим многоугольником.

Задание: Докажите, что многоугольник является выпуклым тогда и только тогда, когда целиком лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Задание: Докажите, что многоугольник является выпуклым тогда и только тогда, когда все его диагонали лежат в многоугольной области.

Очевидно, что выпуклыми могут быть только простые многоугольники.

Задание: Докажите, что многоугольник с самопересечением не является выпуклым.

Задание: Приведите примеры простых выпуклых и невыпуклых многоугольников.

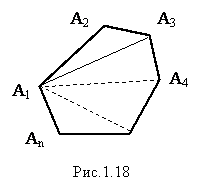
Теорема 1: Сумма углов выпуклого n-угольника равна 180^о(n-2).

Доказательство: Пусть А₁А₂…А_n – данный выпуклый многоугольник (рис. 1.18).

Аn

В случае n=3 теорема справедлива. Пусть n>3. Проведем из вершины А₁ n-3 диагонали: А₁А ₃, А₁А₄, …, А₁А_n-1. Эти диагонали образуют n-2 треугольника: ∆А₁А₂А₃, ∆А₂А₃А₄, …, ∆А₁А_n-1А_n. Сумма углов многоугольника А₁А₂…А_n равна сумме углов всех полученных треугольников и равна 180^о(n-2). Теорема доказана.

Почему теорема не верна для невыпуклых многоугольников? Вернемся к четырехугольнику на рис.1.16.

Если бы величина угла при вершине C была равна ÐACB+ÐACD, то сумма углов четырехугольника была бы равна 360^о и утверждение о сумме углов было бы верным.

5.3.3 Внутренние углы многоугольника.

До сих пор мы имели дело с углами, которые называются линейными. Раньше мы их называли просто углами, потому что другие виды углов не рассматривались. Сейчас же появилась необходимость ввести новый вид угла – плоский угол.

Плоский угол – это часть плоскости, ограниченная сторонами линейного угла.

Не всякий линейный угол ограничивает часть плоскости, а только тот, сторонами которого являются лучи. Такой линейный угол задает два плоских угла (рис.1.19).

Плоские углы с общими сторонами называются дополнительными.

Как на рисунке отличить плоский угол от линейного? Если линейный угол отмечают поперечиной (рис.1.20.а), то плоский угол принято отмечать дугой (рис.1.20.б).

Вопрос для дискуссии: Как измерять плоские углы?