Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 14

Нет (рис. 2.9).

Вопрос для общеклассной дискуссии: Какому дополнительному условию должен удовлетворять четырехугольник с равными сторонами, чтобы быть прямоугольником?

Задание: Сформулируйте и докажите признак прямоугольника через его диагонали.

§ 2.4 Ромб

2.4.1 Свойства ромба

Ромбом называется четырехугольник, у которого все стороны равны (рис. 2.10).

Какие свойства имеет ромб?

Построим произвольный равносторонний четырехугольник ABCD (рис.2.11). Если в нем провести диагональ АС, то получатся два равных равнобедренных треугольника ∆ABC и ∆ADC (рис. 2.12).

В силу равенства треугольников ∆ABC и ∆ADC и свойства углов равнобедренного треугольника углы ÐBAC, ÐBCA, ÐDAC и ÐDCA равны. Из этого следует, что

a) диагональ АС – биссектриса углов ÐВАD и ÐВСD;

b) прямые АВ и СD параллельны;

c) прямые ВС и АD параллельны.

Последние два пункта говорят о том, что ромб АВСD – параллелограмм.

Продолжим наше исследование.

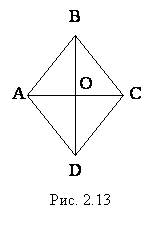Пусть О – точка пересечения диагоналей АС и ВD ромба АВСD (рис.2.13).

Треугольники AOB, AOD, COB, COD равны по первому признаку. Действительно, AB=BC=CD=DA по определению ромба, а OB=OD и AO=OC по свойству диагоналей параллелограмма.

Из равенства треугольников следует равенство их соответствующих углов. А это означает, что диагонали ромба перпендикулярны и являются биссектрисами его углов.

Задание: Оформите в виде теорем свойства диагоналей ромба.

Следствие. Биссектриса угла, лежащего против основания равнобедренного треугольника, перпендикулярна основанию и делит его пополам.

2.4.2 Признаки ромба

Могут ли диагонали четырехугольников, которые не являются ромбами, пересекаться под прямым углом или быть биссектрисами всех углов?

Взгляните на рисунок 2.14. На нем изображен четырехугольник, диагонали которого перпендикулярны. Вы видите, что он не является ромбом.

Задание: Наложите на четырехугольник дополнительные ограничения, чтобы он стал ромбом. Результат запишите в виде теоремы.

Нужно ли на четырехугольник, чьи диагонали являются биссектрисами его углов, накладывать ограничения, чтобы он стал ромбом?

Пусть у четырехугольника АВСD (рис. 2.15) углы ÐСАВ и ÐСАD, ÐBCA и ÐDCA попарно равны. Тогда треугольники АВС и АDC равны по второму признаку. Это значит, что АВ=АD и ВС=DC.

Треугольники ∆BCD и ∆BAD – равнобедренные. По свойству углов равнобедренного треугольника ÐCBD=ÐCDB, ÐABD=ÐADC. Если диагональ BD является биссектрисой углов, тогда ÐCBD=ÐCDB=ÐADB=ÐABD. У нас получилось, что треугольники ABD и CBD равны по второму признаку. Отсюда следует равенство сторон AB, BC, CD и DA. Следовательно, четырехугольник ABCD – ромб.

Мы выяснили, что четырехугольник, у которого диагонали являются биссектрисами его углов, является ромбом. Осталось оформить это в виде теоремы.