Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 13

2.2.2 Параллелограмм

Трапеция с параллельными боковыми сторонами называется параллелограмом (рис. 2.4).

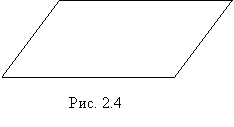Более распространенное определение параллелограмма звучит следующим образом: параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Задание: Докажите эквивалентность обоих определений параллелограмма.

Параллелограмм не является для вас новой фигурой. Вы сталкивались с ним в 7 классе при изучении взаимного расположения четырех прямых. А именно, параллелограм получался при пересечении двух параллельных прямых двумя другими параллельными прямыми (рис. 2.5).

 Задание: Вспомните свойства параллелограмма.

Вопрос для общеклассной дискуссии: Так как у параллелограмма пртиволежащие стороны попарно равны, он является трапецией с равными боковыми сторонами и трапецией с равными основаниями. Но любая ли равнобокая трапеция или трапеция с равными основаниями будет параллелограммом?

Итак, параллельность противолежащих сторон влияет на отношения противолежащих сторон и отношения противолежащих углов. А влияет ли параллельность сторон на отношения соседних сторон и углов? Предлагаем этот вопрос для общеклассной дискусии.

Как сказывается параллельность сторон на диагоналях параллелограмма?

Задание: Нарисуйте несколько параллелограммов, имеющих одну общую диагональ. Проведите у всех параллелограммов по второй диагонали. Какой вывод вы можете сделать, глядя на свои рисунки?

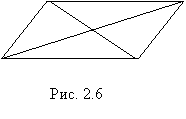
Теорема. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Доказательство теоремы вы сможете “прочитать” по рисунку 2.6.

Вопрос для общеклассной дискуссии: Существуют ли отличные от параллелограмма четырехугольники, диагонали которых точкой пересечения делятся пополам?

§ 2.3 Прямоугольник

Прямоугольником называется четырехугольник, у которого все углы прямые (рис. 2.7).

Сумма любых двух соседних углов прямоугольника равна 180^о. Это говорит о том, что противолежащие стороны прямоугольника попарно параллельны. Значит, прямоугольник является параллелограммом и, как следствие, обладает всеми его свойствами.

Проведем в прямоугольнике АВСD диагонали (рис. 2.8).

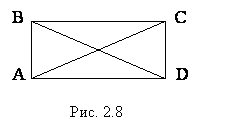Видно, что диагонали АС и ВD равны. Докажем это.

Теорема. Диагонали прямоугольника равны.

Доказательство. Пусть дан прямоугольник АВСD с диагоналями АС и ВD (рис. 2.8). Рассмотрим прямоугольные треугольники АВС и DСВ. У них сторона ВС – общая, стороны АВ и СD равны как противолежащие стороны прямоугольника, углы АВС и DВС прямые. Отсюда следует, что треугольники АВС и DВС равны. Из равенства треугольников следует равенство их сторон АС и ВD, которые являются диагоналями прямоугольника АВСD. Теорема доказана.

Сформулируем обратное теореме утверждение: “Если диагонали четырехугольника равны, то этот четырехугольник – прямоугольник”. Является ли данное утверждение верным?