Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 19

§ 4.2 Объяснительная записка к главе «Ломаная»

1. Следуя логике получения треугольника в учебнике «Геометрия 7» [2], мы должны получить многоугольник при пересечении нескольких прямых. Однако авторы многих учебников – Погорелов А.В. [17], Щетников А.И. [24], Шарыгин И.Ф. [21], вводят понятие многоугольника через ломаную. Мы задались вопросом, насколько это принципиально. 

Исследуя способ получения многоугольника путем пересечения прямых, мы отказались от него. Переход от n прямых к n–угольнику оказался сложным. Следующий анализ подтверждает это.

Разберем для простоты случай пересечения четырех прямых. Все возможные варианты пересечения четырех прямых показаны на рис. 4.1. (Мы не рассматриваем случаи пересечения всех прямых в одной точке и пересечения трех параллельных прямых четвертой, так как они  не дает многоугольников):

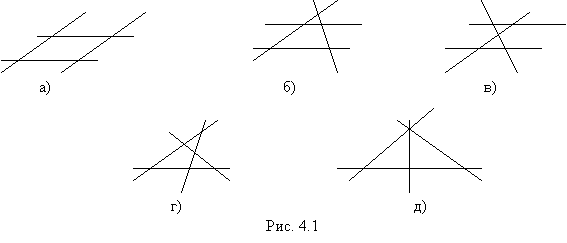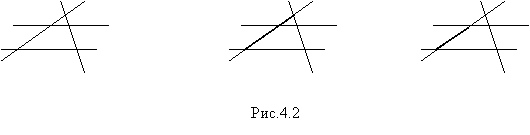
 При пересечении четырех прямых мы должны получить четырехугольник. Но, как видно из рис.4.1, только при пересечении двух параллельных прямых двумя другими параллельными прямыми (рис.4.1.а) можно смело утверждать, что действительно получен четырехугольник. В других случаях кроме четырехугольника получаются еще и треугольники. Например, в случае 4.1.б) образовалось два треугольника и один четырехугольник (рис.4.2).

Допустим, что, сославшись на изученность треугольника, будем рассматривать только новые фигуры - четырехугольники. Но тогда при введении четырехугольников логика выделения фигуры из пересечения прямых будет отличаться от логики выделения треугольника.

Действительно, когда мы пересекаем три прямые, то для получения треугольника точки пересечения прямых и отрезки, заключенные между ними, считаем равноправными. Если при пересечении четырех прямых все точки считать равноправными, то лишь случаи 4.1.а) и 4.1.д) дадут нам четырехугольники. Чтобы и в других случаях получить четырехугольники, надо одни точки пересечения прямых предпочесть другим (рис.4.3).

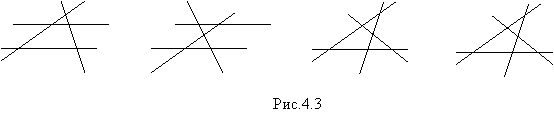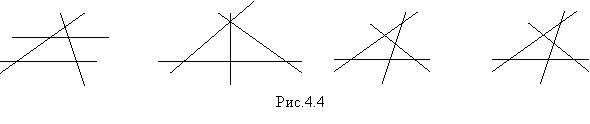
С отрезками та же ситуация. Все отрезки равноправны у четырехугольников на рисунке 4.1.а), 4.1.в). В других случаях одни отрезки предпочитаются другим (рис.4.4).

 Итак, во всех случаях пересечения четырех прямых, кроме 4.1.а), для введения четырехугольника требуется изменить логику выделения фигуры. Новая логика значительно сложнее логики выделения треугольника, так как критерием выделения фигуры является ее новизна.

 Случай 4.1.а) является особым: здесь четыре прямые пересекаются в четырех разных точках. Для пяти и более прямых случай, подобный 4.1.а), невозможен.

Таким образом, наш анализ подтвердил оправданность введения многоугольника через ломаную.

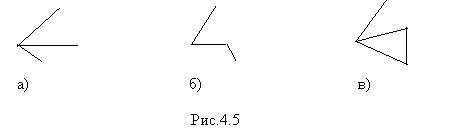
2. При введении представления о ломаной мы столкнулись с проблемой определения ломаной: считать ломаной последовательность соединенных концами отрезков или множество соединенных концами отрезков. Разница обоих подходов видна на рис.4.5.

Каждая фигур на рис.4.5 представляет собой множество соединенных концами отрезков. Но фигуры 4.5.б) и 4.5.в) можно представить как последовательность соединенных концами отрезков, а фигуру 4.5.а) - нельзя.