Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 5

Задание: Вспомните, какие геометрические фигуры называются основными и составными. Как они были получены? Какие геометрические фигуры вы знаете? Вспомните их определения.

§ 5.1 Ломаная

5.1.1 Фигура, имеющая длину

Из всех основных геометрических фигур только отрезок обладает такой характеристикой как длина. Почему так? Длина – это некоторая количественная характеристика. Для ее нахождения нужно иметь возможность измерить. Для этого нужна мерка, начало и конец. А из основных фигур только отрезок как изображение процесса измерения произвольной меркой заданной величины обладает ими. При этом, если мы различаем направленность процесса измерения, говорим о начале и конце отрезка (в подробном описании). Иначе говорим (обобщенно) о концах отрезка.

Может ли составная фигура иметь длину? Да, если она состоит из отрезков и имеет начало и конец (обобщенно – 2 конца).

Рассмотрим случаи фигур, состоящих из двух отрезков (рис. 1.1).

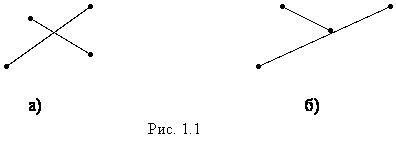Фигура 1.1.а) имеет 4 конца. А сколько концов имеет фигура 1.1.б)? Мы считаем, что у фигуры 1.1.б) 3 конца.

Фигуры на рисунке 1.1 имеют больше двух концов, следовательно, мы не можем говорить о их длине.

Задание: Нарисуйте фигуру из двух отрезков, имеющую два конца. Сколько начал и концов имеет ваша фигура?

Фигура, составленная из двух отрезков, имеет одно начало и один конец в том случае, когда конец одного из них служит началом другому. Другими словами, фигура из двух отрезков имеет длину, если представляет собой последовательность соединенных концами отрезков (рис. 1.2).

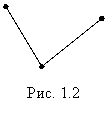Теперь составим из трех отрезков фигуру, имеющую длину. Для этого соединим последовательно концами два отрезка. В силу приведенных выше рассуждений полученная фигура имеет длину. Куда нужно поместить третий отрезок? А куда его можно поместить?

Задание: Нарисуйте три отрезка и нарисуйте несколько вариантов составленных из них фигур, имеющих длину.

У вас наверняка есть фигуры как 1.3.а). А есть ли среди ваших вариантов такие (рис. 1.3.б, 1.3.в, 1.3.г)?

Какие точки каждой из фигур на рисунке 1.3 можем считать началом и концом?

Вопрос для общеклассной дискуссии: Из скольких отрезков может состоять фигура, имеющая длину?

Дадим определение (генетическое) фигурам, имеющим длину.

Фигура, которую можно представить в виде последовательности соединенных концами отрезков, называется ломаной.

Длина ломаной равна сумме длин отрезков, ее составляющих.

5.1.2 Структурное определение ломаной.

Чтобы дать структурное определение ломаной, нужно выделить ее компоненты и назвать их.

Отрезки, составляющие ломаную, называются звеньями ломаной.

Достаточно ли звеньев ломаной для того, чтобы дать структурное определение ломаной? Нет, потому что у ломаной звенья последовательно соединены. Следовательно, точки соединения звеньев надо тоже отнести к компонентам ломаной. А как быть с началом и концом ломаной? Они тоже особые точки. Благодаря им мы можем говорить о длине ломаной. Имеет смысл ввести обобщенное название для точек соединения звеньев и концов ломаной – вершина ломаной.

Вопрос для дискуссии на предметной мастерской: В чем смысл введения подробных и обобщенных названий?