Пробное учебное пособие по темам «Ломаная», «Четырехугольник», «Площадь» для восьмого класса, страница 7

5.1.5 Соотношение звеньев и вершин ломаной.

Соотношение звеньев и вершин – это практически соотношение отрезков и точек. А мы знаем, что точки могут лежать на отрезке или не лежать на нем.

На любом звене ломаной лежит две вершины (в них звено соединяется с другими звеньями). А может на звене лежать больше двух вершин? Может, и в этом случае мы говорим о точках самокасания ломаной.

Задание: Выяснить, является ли точка самокасания отличным от ранее рассмотренных элементом ломаной.

§ 5.2 Многоугольник.

Мы получили простые и замкнутые ломаные, рассматривая  соотношения звеньев и вершин. Это были соотношения взаимного расположения. А какие еще бывают соотношения?

 Численные. Эти соотношения для вас не новы. Вы с ними сталкивались, когда, например, определяли, в каких соотношениях находятся длины двух отрезков или площади двух прямоугольников (рис.1.7).

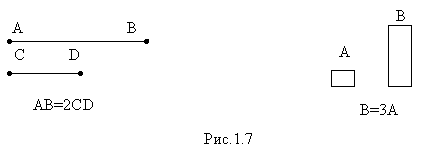Численные соотношения находятся для некоторых характеристик фигур – численных характеристик (параметров).В приведенных примерах параметрами (численными характеристиками) являются соответственно длины отрезков и площади фигур.

Какие параметры имеет ломаная? Попробуем ответить на вопрос, сравнивая две ломаные (рис.1.8).

Как и в случае отрезков, мы можем сравнить эти ломаные по длине. Так как ломаные состоят из разного числа звеньев и вершин, то мы можем сравнивать ломаные и по этим параметрам – числу звеньев, числу вершин.

Мы выделили три параметра ломаной: длина, число звеньев и число вершин. Есть ли у ломаной другие численные характеристики? Предлагаем этот вопрос для общеклассной дискуссии.

5.2.1 Соотношение параметров ломаной.

Есть ли какая-нибудь связь между выделенными тремя параметрами ломаной? Очевидно, что длина ломаной в общем случае не зависит от числа ее звеньев. Но, если звенья одинаковой длины, то чем больше звеньев имеет ломаная, тем больше ее длина.

Ломаная с равными звеньями называется равнозвенной.

Задание: Приведите примеры ломаных с равной длиной, состоящие из разного количества звеньев.

Длина ломаной также не зависит и от числа вершин.

А как связаны между собой число звеньев и число вершин?

У однозвенной ломаной вершин на одну больше, чем звеньев. У двузвенной ломаной и у ломаных на рис.1.8 то же самое соотношение числа вершин и числа звеньев. Может ломаная иметь другие численные соотношения звеньев и вершин?

Задание: Приведите, если это возможно, примеры ломаных с другими соотношениями чисел звеньев и вершин.

Все ломаные, приведенные нами выше в качестве примеров, являются простыми и для них справедливо соотношение: вершин на одну больше, чем звеньев. Можно ли на основе этого сделать вывод, что у каждой простой ломаной вершин на одну больше, чем звеньев, и обратно: ломаные, у которых вершин на одну больше, чем звеньев, являются простыми?

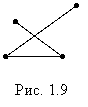Рисунок 1.9 показывает, что данное соотношение звеньев и вершин могут иметь и ломаные с самопересечением.

Задание: Привести примеры ломаных с двойным и тройным самопересечением, у которых вершин на одну больше, чем звеньев.

Можно ли как-то описать класс ломаных, у которых вершин на одну больше, чем звеньев?

Вы наверно заметили, что в данный класс попадают незамкнутые ломаные. А замкнутые ломаные могут в него входить? Предлагаем вам ответить на этот вопрос.