Динамика жесткой машины с одной степенью подвижности

Глава 2.  ДИНАМИКА ЖЕСТКОЙ МАШИНЫ

 С ОДНОЙ СТЕПЕНЬЮ ПОДВИЖНОСТИ

2.1.  Кинетическая энергия машины.  

Приведенный момент инерции

Рассмотрим машину, состоящую из механизмов с жесткими звеньями и приводимую в движение одним двигателем. Ее механическая система обладает  одной  степенью  свободы.  В качестве  обобщенной координаты выберем координату выходного звена двигателя q (рис. 2.1). Определим кинетическую энергию Т машины как системы N материальных точек с массами m₁,…, m_k,…, m_N, на движение которых наложены голономные стационарные связи, обусловленные жесткостью звеньев и наличием кинематических пар. Как известно,

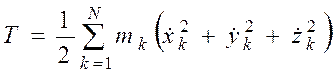,                              (2.1)

где     x_k, y_k, z_k – декартовы координаты k-й материальной точки (проекции радиус-вектора точки на оси координат).

k mk                       Z                                                                      Pk                                                        x y Рис. 2.1. Механическая система с одной степенью свободы

В системе с одной степенью свободы координаты всех точек могут быть представлены как функции обобщенной координаты:

x_k =x _k(q);       y_k =y _k(q);    z_k =z _k(q).                       (2.2)

Дифференцируя (2.2) по времени, находим

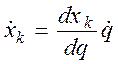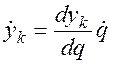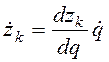;  ; .                                (2.3)

Подставляя (2.3) в (2.1), получаем

.

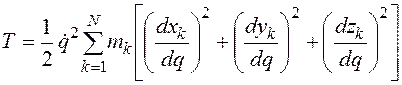Выражение

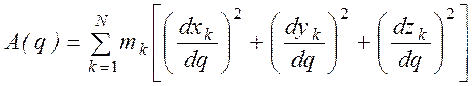                    (2.4)

называется приведенной массой (в случае, если q– линейная координата) или приведенным моментом инерции (если q -  угловая координата) механической системы (механизма) с одной степенью свободы.

Если q – угловая координата, приведенный момент инерции будем обозначать через J(q).

Из выражения (2.4) видно, что для определения приведенной массы или приведенного момента необходимо знать первые производные от координат точек механической системы по обобщенной координате.

Структура приведенного момента инерции. Исследуем структуру приведенного момента  инерции в самом общем случае, когда и двигатель и механическая система содержат механизмы с нелинейными функциями положения. Рассмотрим кинематическую схему машины, представленную на рис. 2.2. Здесь одноцилиндровый поршневой двигатель, в котором выходной вал 1, соединен передаточным механизмом 2 с входным валом 3 исполнительного механизма. Момент инерции всей механической системы может быть представлен в виде суммы момента инерции движущихся частей двигателя и приведенного момента инерции остальных механизмов машины:

.                                     (2.6)

q                             q                                                                                           i     Рис. 2.2. Кинематическая схема машины

Первое слагаемое, очевидно, является периодической функцией угла поворота выходного вала двигателя с периодом 2p, поскольку после поворота этого вала на угол 2p все звенья механизма двигателя возвращаются в исходное положение. Входной вал исполнительного механизма совершает полный оборот при изменении q на 2pi, где i – передаточное отношение между валами 1 и 3. Поэтому второе слагаемое в (2.6) имеет период 2pi. В дальнейшем будет удобно представлять периодические функции J_Д(q) и

J_м(q) в следующем виде:

;    ,                     (2.7)

где ,  - периодические функции с нулевыми средними значениями; J_д0, J_м0 – средние за период значения (постоянные составляющие) моментов инерции:

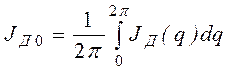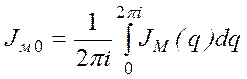;   .                  (2.8)

Подставляя (2.7) в (2.6), имеем

,            (2.9)

где     J₀ =J_Д0 +J _М0– среднее значение момента инерции всей машины.

2.2. Определение обобщенных сил

Для составления управления движения механической системы в форме уравнений Лагранжа второго рода необходимо, кроме кинетической энергии, определить обобщенные силы, соответствующие всем активным силам.

К активным силам относятся движущие силы, прикладываемые к выходному звену двигателя, силы полезного сопротивления, связанные с выполнением рабочего процесса, силы тяжести звеньев механизмов, силы, создаваемые упругими элементами, обеспечивающими замыкание высших кинематических пар, и т.п. В дальнейшем будем выделять обобщенную движущую силу. Предполагая, что обобщенная координата q является углом поворота выходного звена двигателя, будем считать, что обобщенная движущая сила представляет собой момент М_Д, создаваемый двигателем. Зависимость этого момента от параметров движения создается характеристикой двигателя. Остальные активные силы, приложенные к звеньям механизмов, будем в совокупности называть силами сопротивления. Пусть силы сопротивления Р₁,…,P_k (k = 1,…,m) приложены к звеньям механизмов в точках, радиус-векторы которых r₁(q),…,r_k(q) (k =1 ,…,m). Тогда при изменении обобщенной координаты q на  эти силы совершают работу