Динамика жесткой машины с одной степенью подвижности, страница 5

>0.                                                                                                                (2.24)

Если же момент Д_Д(t) окажется знакопеременным, то это приведет к изменению направления передаваемого зубчатыми колесами момента, а, следовательно, и к перекладке зазоров в зубчатых передачах: каждый зубец будет входить в зацепление то одним, то другим своим профилем. Перекладка зазоров – нежелательное явление, приводящее к снижению работоспособности передачи, поэтому выполнение условия (2.24) обычно считается необходимым.

Из всего сказанного следует, что для равномерного вращения входного звена механической системы машины необходимо прикладывать к этому звену переменный вращающий момент, или, иными словами, равномерное вращение входного звена вызывает появление переменного динамического момента. Это важное свойство механизмов будем в дальнейшем называть их внутренней виброактивностью. Переменный момент L(t) может рассматриваться как мера внутренней виброактивности механизма.

2.5.  Исследование установившегося движения с учетом

статической характеристики двигателя

Метод последовательных приближений. Как было показано выше, исследование движения машины сводится в этом случае к интегрированию уравнения (2.20). Установившимся движениям соответствуют так называемые стационарные решения этого нелинейного дифференциального уравнения второго порядка. В нелинейной механике известно множество методов приближенного решения нелинейных уравнений и, в частности, методов отыскания стационарных (установившихся) решений. Воспользуемся здесь методом последовательных приближений.

Мы не будем ставить вопрос о строгом математическом обосновании  метода. Ограничимся лишь эвристическими соображениями, вполне приемлемыми при решении прикладных задач.

В основе метода последовательных приближений лежит предположение о малом отличии угловой скорости  от некоторого среднего значения w₀. Это предположение заложено в введенное определение понятия «установившееся движение». Используя выражения (2.7), (2.9), (2.14), (2.18), а также учитывая, что при установившемся движении u=u₀=const, запишем уравнение (2.20) в виде

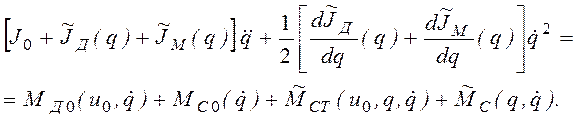                                                                                                                (2.25)

Нетрудно понять, что источником неравномерности вращения выходного звена двигателя является присутствие в уравнении (2.25) слагаемых, явно зависящих от угла поворота  q. Если бы таких слагаемых не было, т. е. если бы момент инерции машины оставался постоянным, а моменты  и  отсутствовали, в системе осуществлялся бы режим равномерного вращения. Действительно, тогда уравнение (2.25) записалось бы в виде

.                                                                                                                (2.26)

Это уравнение может иметь решения вида , , для чего значения  должны удовлетворять условию

.                                                                                                                (2.27)

Иными словами, если существует такая постоянная угловая скорость, при которой сумма момента движущих сил и приведенного момента сил сопротивления равна нулю, то эта угловая скорость является решением уравнения (2.26). Зависящие от q слагаемые в (2.25) приводят к отклонению угловой скорости от постоянного значения, но, по предположению, в установившемся режиме такое отклонение является незначительным. Поэтому попытаемся разыскивать решение уравнения (2.25) методом последовательных приближений, выбрав в качестве исходного (нулевого) приближения решение уравнения (2.26). Перепишем уравнение (2.25) в виде

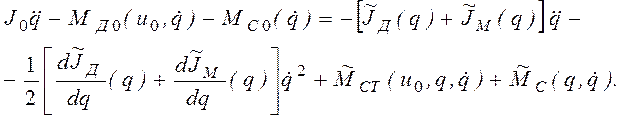                                                                                                                   (2.28)

Определив из уравнения (2.26) нулевое приближение

  ,

подставим его вместо ,  и  в правую часть (2.28) и найдем решение полученного уравнения, правая часть которого является функцией времени:

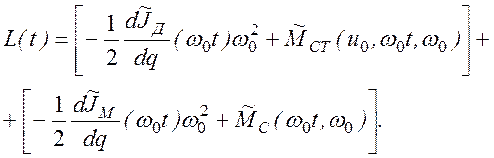                                                                                                                (2.29)