Динамика жесткой машины с одной степенью подвижности, страница 24

Величина

называется перерегулированием переходного процесса.

Если v<<s, то можно положить , и полученные выше формулы упрощаются. В частности, условие возникновения колебательного режима примет вид

<.

Перерегулирование при разбеге для этого случая

,

а время разбега можно приближенно оценить по формуле

Превышение значения  в процессе разбега обычно является нежелательным. Чтобы избежать этого, можно либо увеличить отношение  (например, за счет увеличения J₀), либо использовать двигатель c нелинейной статической характеристикой, в котором крутизна s является малой при малых значениях ω и возрастает в области рабочих скоростей (рис. 2.21), либо применить управляемый разбег, при котором величина u(t) постепенно нарастает до u₀, обеспечивая плавное изменение угловой скорости. Во всех случаях изменение характера разбега сопровождается увеличением его продолжительности.

М                                                                  М_П

                                                                       М₀

 М₀

 

                                                            

 

0                                                          0                              t

Рис. 2.21. Билинейная статическая              Рис. 2.22. Закон изменения

характеристика двигателя                          М_П(t) при разбеге:

                                                            1 - >; 2 - <

Определим закон изменения момента в передаточном механизме при разбеге. Используя первое уравнение (2.103), получаем

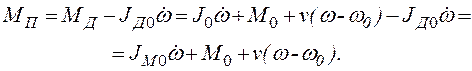                                                                                                              (2.109)

При апериодическом разбеге, подставляя   из (2.107), находим

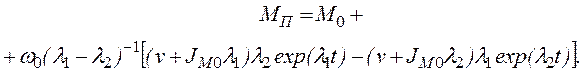                                                                                                                 (2.110)

При t®¥ имеем М_П ® М₀; при t = 0 будет М_П = М₀ - vw₀ (рис. 2.22). Выясним, при каких условиях момент М_П в течение всего процесса разбега остается меньше, чем М₀. Для этого определим экстремальные значения M_П(t). Дифференцируя (2.110) и приравнивая производную нулю, получаем

                                                                                                              (2.111)

где t* - момент достижения экстремума.

Из (2.111)  находим

                                                                                                              (2.112)

Пусть для определенности 0>l₁ >l₂, тогда 0 < exp[(l₁ -l₂)t*] <1 и равенство (2.111) может выполняться лишь в том случае, если v + J_м0 l₁ <0  т.е. если êl₁ê>v. Только в этом случае функция (2.110) имеет экстремум, причем легко показать, что это - максимум. В результате закон изменения Мп(t) может иметь формы, показанные на риc. 2.22. Таким образом, Мп(t)<Мо, если êl₁ê<v|.

Закон изменения Мп(t) при колебательном разбеге примет вид

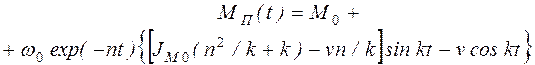                                                                                                              (2.113)

В этом случае максимальное значение Мп(t) всегда превосходит значение М₀.

Учет возмущений. Законы изменения угловой скорости при разбеге были получены при усреднении за оборот ротора сил, зависящих от координаты q, что привело к приравниванию нулю членов, стоящих в правых частях уравнений (2.28) и (2.81). Можно, однако, рассматривать полученные решения как приближенные и построить на их основе процесс последовательных приближений, аналогичный тому, который использовался в
п. 2.4. Иными словами, можно учесть влияние возмущений на процесс разбега.

Рассмотрим, каким образом это можно сделать в случае линейных характеристик  и , и при учете динамической характеристики двигателя. Запишем уравнение движения машины (2.109), заменив Мдо и М_СО их линейными представлениями:

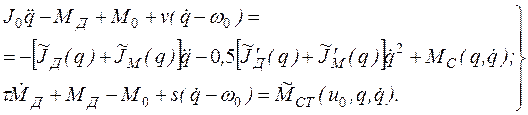                                                                                                        (2.114)

Подставим в правые части уравнений (2.114), найденные выше решения уравнений (2.103), положив в них

        .

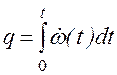Получим систему однородных линейных уравнений:

.