Динамика жесткой машины с одной степенью подвижности, страница 22

Будем предполагать, что разбег совершается достаточно медленно: так, что за каждый оборот вала двигателя (т. е. при изменении q на 2p) средняя угловая скорость изменяется незначительно. Будем сначала полагать, что при этом допущении можно пользоваться для исследования разбега статической характеристикой двигателя. Тогда задача сводится к интегрированию уравнения (2.20) при нулевых начальных условиях. Перепишем это уравнение в форме (2.28). Медленность изменения  позволяет в первом приближении заменить, правую часть этого уравнения  его средним за оборот значением, которое в силу определения функций  равно нулю. Таким образом, в первом приближении задача сводится к интегрированию уравнения (2.26) при условии  (0) = 0. Уравнение (2.26) интегрируется в квадратурах. Обозначив   = w, получим из (2.26)

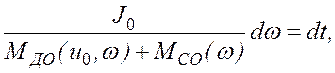
или 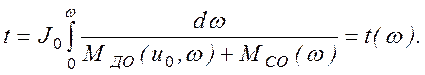                      (2.98)

Обращением этой функции получаем зависимость w(t). Время разбега t_p можно определить, положив в (2.12) верхний предел равным w₀:

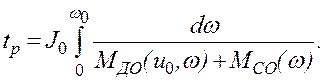
Поскольку  [см. (2.27)], этот интеграл является несобственным. Можно показать, что при s + v¹ 0 величина t_p стремится к бесконечности. Учитывая это, обычно время разбега определяют как время достижения угловой скорости, близкой к w₀, но не равной ей. Чаще всего условно принимают, что

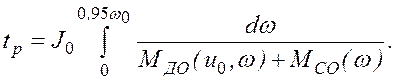                                                                                                                (2.99)

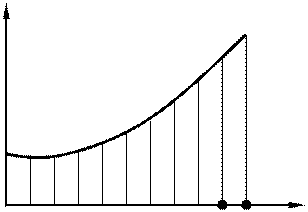
Величину t_p и закон изменения w(t) можно определить, например, графическим способом, построив график зависимости (рис. 2.17)

Площадь фигуры, заштрихованной на рисунке, соответствует t_p.

Из формулы (2.99) видно, что время разбега пропорционально J₀, поэтому уменьшение J₀ является одним из наиболее эффективных методов уменьшения времени разбега. Для многих машин, в которых процесс разбега занимает значительную часть рабочего времени (например, для металлорежущих станков), это приводит к  существенному увеличению производительности.

            

                                                   

                      0                          0,95       

Рис. 2.17. Графическое определение времени разбега

Определение времени разбега при линейных характеристиках. Определим время разбега машины в случае линейных характеристик:

                                                                   (2.100)

где

Подставим (2.100) в (2.26), получим

Определяя общее решение этого линейного дифференциального
уравнения, имеем

Из начальных условий определяем постоянную интегрирования С:

       

Отсюда

                                                                                                              (2.101)

Полагая w= 0,95w₀, находим

Таким образом, постоянная времени t_M полностью определяет время разбега машины при линейных характеристиках. Для уменьшения t_p нужно либо уменьшать J₀, о чем уже говорилось выше, либо увеличивать крутизну s характеристики двигателя.

Оценим среднее приращение угловой скорости за один оборот двигателя. Для этого определим угол поворота ротора за время разбега

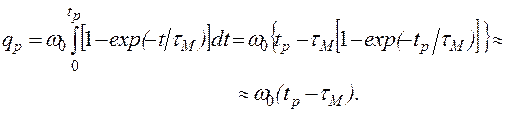
Если t_p » 3t_м ,то q_p » 2w₀t_м. Тогда среднее приращение угловой скорости за один оборот

Для того чтобы усреднение правой части уравнения (2.28) оказалось допустимым, характеристики  и  должны мало изменяться при изменении  на эту величину.

Определение момента в передаточном механизме. Найдем  момент М_П, возникающий в передаточном механизме при разбеге. Составив уравнение движения механической системы

и учтя выражение (2.101), получим

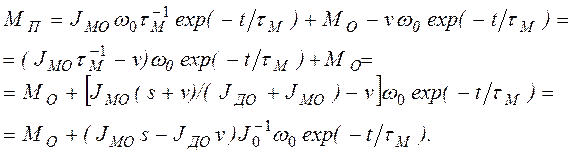
В зависимости от знака разности  закон изменения М_П(t) может иметь различную форму (рис. 2.18). Очевидно, что для передаточного механизма предпочтительнее тот случай, когда М_П(t) £M₀, т.е. когда J_МОs<, или v/s>

В общем случае при произвольных нелинейных характеристиках М_ДО и М_СО из уравнения (2.26) находим

Отсюда