Динамика жесткой машины с одной степенью подвижности, страница 13

Один из простейших гасителей показан рис. 2.10,a. Он  состоит из дополнительной массы, устанавливаемой обычно на выходном валу передаточного механизма, и пружины кручения, соединяющей ее с этим валом.

Полагая, что момент инерции гасителя равен J_r, а жесткость пружины с_r составим уравнение движения машины с гасителем. При колебаниях массы гасителя относительно вала возникает упругий момент, действующий на вал и равный , где  - угол поворота массы гасителя относительно вала (угол закручивания пружины). Вводя этот момент в уравнение возмущенного движения машины (2.44), получим

.                                                                                                                (2.56)

С другой стороны, движение массы гасителя можно представить уравнением вращательного движения твердого тела

,                                                                                                                (2.57)

где  — абсолютное угловое ускорение массы J_r.

Для определения стационарного решения системы уравнений (2.56) и (2.57) запишем их в операторной форме:

;

.

Разрешая эти уравнения относительно неизвестной , получаем

.

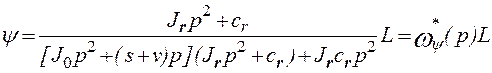Пусть мы стремимся исключить из динамической ошибки  гармонику частоты v. Тогда необходимо, чтобы амплитудно-частотная характеристика

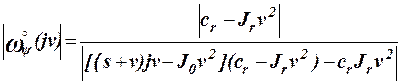
равнялась нулю. Очевидно, что это достигается, если выбрать с_r и J_r с таким расчетом, чтобы . Таким образом, с помощью динамического гасителя можно компенсировать действие одной из гармоник возмущающего момента.

Из-за наличия сил сопротивления, действующих на гаситель, в действительности  компенсация оказывается неполной. Кроме того, амплитуды остальных гармоник колебательной составляющей закона движения изменяются мало. Поэтому динамические гасители целесообразно применять в тех случаях, когда одна из гармоник превалирует над остальными.

Рассмотрим другой вариант динамического гасителя рис. 2.10,б. Ползун массой m приводится в движение силой F, к ползуну присоединена масса  m_r с помощью пружины жесткостью с. Найдем, как связана сила F с законом движения ползуна х₁(t). Уравнение движения ползуна запишем в виде

,                                                                                                                (2.58)

где     x₂ -  перемещение массы гасителя.

С другой стороны,

.                                                                                                                (2.59)

Определив x₂  из (2.59) и подставив его в (2.58), получим:

;  ;

.

Отсюда

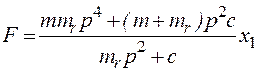.                                                                                                                (2.60)

Если выбратьс и т_rтак, чтобы

,                                                                                                                (2.61)

то при движении ползуна по закону  сила F(t) станет тождественно равной нулю.

Применяя разгружатели и динамические гасители, необходимо
учитывать следующие обстоятельства.

1) Разгружатели и гасители оказываются наиболее эффективными в тех случаях, когда средняя угловая скорость  остается практически постоянной. При изменении угловой скорости происходит «расстройка» динамического гасителя, поскольку его парциальная частота  уже не будет совпадать с частотой v. Снижается и эффективность кулачковых разгружателей, так как при изменении  момент L_М(t) существенно изменяется (в частности, из-за наличия слагаемого, пропорционального ), а разгружающий момент изменяется незначительно. В результате суммарный момент отличается от нуля.

2) Введение разгружающего механизма из-за наличия в нем сил трения приводит к увеличению среднего момента сил сопротивления. Тем самым увеличивается и нагрузка на двигатель.