Динамика жесткой машины с одной степенью подвижности, страница 7

>0.                                                                                                                (2.33)

Геометрически это означает, что в точке  (рис. 2.5) тангенс угла наклона касательной к характеристике – М_С0(q) должен быть больше, чем тангенс угла наклона касательной к характеристике среднего движущего момента.

Решение уравнения (2.28), близкое к неустойчивому решению уравнения (2.26), если оно и существует, окажется также неустойчивым, а, следовательно, и нереализуемым. Поэтому отыскание  дальнейших приближений должно производиться только для устойчивых равномерных вращений.

Предположим, что вследствие изменения параметров рабочего процесса или других сил сопротивления средний момент М_Д0 получил некоторое малое постоянное приращение . Из рис. 2.5 легко определить, что при этом угловая скорость равномерного вращения получит приращение

.

Величину

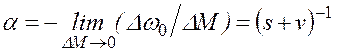                                                                                                                (2.34)

будем называть коэффициентом чувствительности или просто чувствительностью исследуемого режима к изменению нагрузки.

Чувствительность является важнейшей характеристикой режима установившегося движения машины. Большая чувствительность означает, что малые изменения сил сопротивления (или движущих сил), неизбежные в реальной машине (например, изменение сил трения, вызванное колебаниями температуры смазочной жидкости), могут приводить к существенным изменениям угловой скорости . Как правило, такие явления недопустимы, и в подобных случаях принимаются меры для уменьшения чувствительности. Одной из таких мер является введение регулятора скорости: при уменьшении угловой скорости, вызванном изменением нагрузки, регулятор увеличивает значение входного параметра двигателя и тем самым смещает его характеристику (штриховая линия на рис. 2.5), восстанавливая требуемое значение угловой скорости. Другой способ понижения чувствительности состоит в присоединении к двигателю коробки скоростей или вариатора - передаточного механизма с изменяемым передаточным отношением. При увеличении момента сил сопротивления передаточное отношение увеличивают, тем самым увеличивается и момент движущих сил на выходном валу передаточного механизма.

Определение первого приближения. Перейдем к определению решения уравнения (2.28) в первом приближении. Подставив в правую его часть устойчивое решение вида , получим функцию L(t), определяемую выражением (2.29). Эта функция представляет собой возмущение, которое и вызывает отклонение движения от равномерного вращения. Как видно из (2.29), возмущение состоит из двух слагаемых. Первое слагаемое представляет собой возмущение, вызванное двигателем (переменностью J_Д и явной зависимостью М_СТ от q):

.                                                                                                                (2.35)

Для роторных двигателей L_Д(t) = 0; в общем случае  L_Д(t) - периодическая функция с периодам , не содержащая постоянной составляющей. Она может быть представлена в виде ряда Фурье

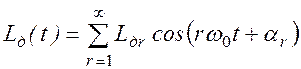.                                                                                                                (2.36)

Второе слагаемое в (2.29)

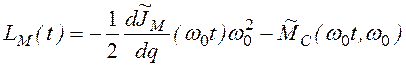                                                                                                         (2.37)

представляет собой возмущение, вызванное исполнительным механизмом и рабочим процессом, происходящим в машине (зависимостью J_М от q и М_С от q). Оно является периодической функцией t с периодом, равным времени одного оборота входного звена исполнительного механизма , где  - угловая скорость этого звена. Раскладывая (2.37) в ряд Фурье, имеем