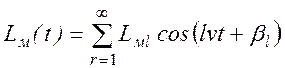Динамика жесткой машины с одной степенью подвижности, страница 8

.                                                                                                                (2.38)

В левой части уравнения (2.28) содержатся нелинейные функции  и , что существенно усложняет его решение. Учитывая, что, в соответствии со сделанными предположениями, значения  изменяются только в малой области, лежащей вблизи , можно провести линеаризацию этих функций, положив

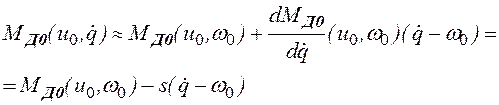;                                                                                                                (2.39)

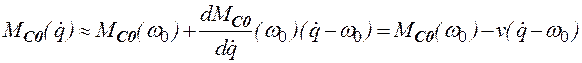.                                                                                                                 (2.40)

Эта линеаризация эквивалентна замене участков характеристик среднего движущего момента и среднего момента сил сопротивления вблизи точки  участками касательных к этим характеристикам.

Учитывая (2.29), (2.39) и (2.40), уравнение (2.28) запишем в виде

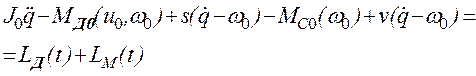         .                                                      (2.41)

Введем новую неизвестную

;    ;    ,                                                                                                                (2.42)

представляющую собой отклонение угла поворота выходного звена двигателя от . Учитывая, что равномерное вращение можно считать для установившегося режима программным движением, функцию  естественно рассматривать как динамическую ошибку по углу, а ее производную  - как динамическую ошибку по угловой скорости. Учитывая также, что  удовлетворяет уравнению (2.27), имеем

.                                                                                                                (2.43)

Установившемуся движению соответствует стационарное частное решение этого уравнения [общее решение однородного уравнения, совпадающего с (2.31), стремится к нулю в силу выполнения условия устойчивости].

Для определения стационарных частных решений линейных дифференциальных уравнений с постоянными коэффициентами будем в дальнейшем пользоваться методом, основанным на введении в рассмотрение передаточных функций и частотных характеристик системы.

В рассматриваемом случае, записав уравнение (2.43) в операторной форме

,                                                                                                                (2.44)

определяем передаточную функцию, связывающую неизвестную функцию  y  с возмущением,

.

Находим амплитудно-частотную и фазочастотную характеристики:

.

.

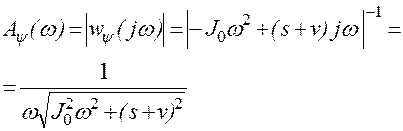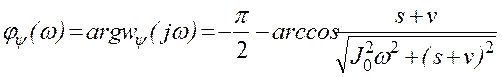Используя принцип суперпозиций, получаем

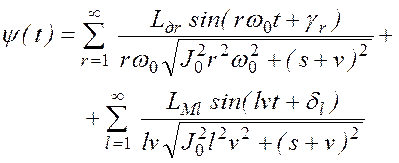,                                                                                                                   (2.45)

где                         ;   .

Продифференцировав (2.45), находим динамическую ошибку по угловой скорости

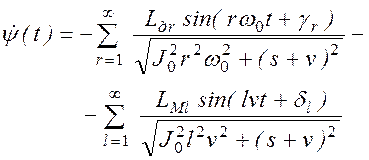                               .                                                          (2.46)

Как уже отмечалось, точность определения динамических ошибок, даваемая первым приближением [формулы (2.45) и (2.46)], обычно оказывается достаточной для практики. Дальнейшие уточнения, связанные с определением второго приближения, как правило, не требуются. Ряды Фурье, входящие в выражения для  и , обычно быстро сходятся. Это объясняется, во-первых, тем, что коэффициенты L_Дr и L_Ml убывают с ростом их номера как коэффициенты сходящихся рядов Фурье; во-вторых, тем, что номера гармоник (г или l) стоят в знаменателях коэффициентов рядов (2.45) и (2.46). В некоторых случаях можно даже ограничиться сохранением в этих рядах только первой гармоники или двух первых гармоник.

В технических требованиях к машине часто задаются допустимые значения максимальных динамических ошибок, обусловливается малая неравномерность вращения выходного вала двигателя. Обычно при этом задается допустимый коэффициент неравномерности

.

Если, например, источником возмущения является только исполнительный механизм [L_Д(t)= 0] и если можно в (2.46) ограничиться сохранением только первой гармоники, т. е. если

,

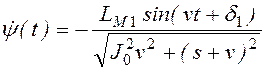то 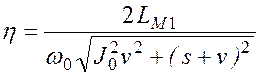                                     .                                          (2.47)

В этом случае легко получается зависимость требуемой постоянной составляющей момента инерции J₀ от допустимого значения .