Динамика жесткой машины с одной степенью подвижности, страница 25

Решая эти уравнения при начальных условиях t = 0; ; , получим уточненные решения для  и М_Д(t). Далее процесс последовательных приближений можно продолжить. Сходимость этого процесса может быть доказана в предположении, что правые части уравнений остаются достаточно малыми при всех t.

2.12. Торможение машины

Торможение машины может производиться различными методами. Чаще всего при торможении двигатель отключается и включается тормоз, создающий дополнительный момент сопротивления М_Т, который обычно может считаться постоянным по величине. Предполагая, что угловая скорость в процессе торможения изменяется медленно, и усредняя правую часть уравнения (2.28), приходим к уравнению движения машины.

.                                                                                                              (2.115)

Необходимо найти решение , соответствующее начальным условиям t = 0; . Интегрируя уравнение (2.115) находим

.

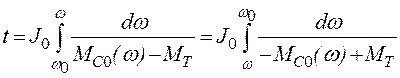Время торможения найдем, положив нижний предел равным нулю:

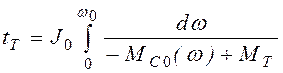.                                                                                                              (2.116)

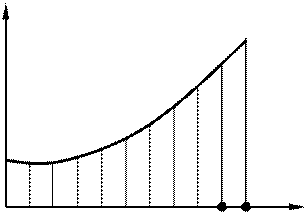
Этот интеграл можно вычислить с помощью графика, аналогичного построенному на рис. 2. 17.

При линейной характеристике  уравнение (2.115) принимает такой вид:

,

или  

,                                                                                                              (2.117)

где     .

            

                                                   

0                          0,95

Рис. 2.17. Графическое определение времени разбега

Общий интеграл уравнения (2.117)

.

Из начальных условий  t = 0 и  находим постоянную C и получаем закон изменения угловой скорости

.                                                                                                              (2.118)

Из условий t = t_T и    определяем время торможения

.

Определим теперь момент в передаточном механизме М_П, предполагая, что тормозной момент прикладывается со стороны двигателя. Составим уравнение движения механической системы машины

.

Отсюда

.

Подставив  из (2.118), получим

.

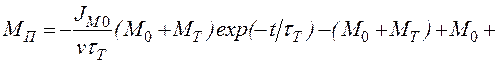
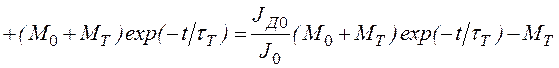При t = 0 имеем ;  получим . В процессе торможения  монотонно изменяется в интервале между этими двумя значениями. Если принять M_T = M₀, то значение  будет меньше, чем М₀. Действительно, при этом

< M₀.

В этом случае момент в передаточном механизме в течение всего процесса торможения окажется меньше, чем средний момент в установившемся режиме, и торможение, таким образом, не будет сопровождаться дополнительным нагруженном передаточного механизма. Время торможения будет равно

.

Случай, когда и v = 0 (средний момент сил сопротивления не зависит от скорости), требует особого рассмотрения. В этом случае из уравнения движения

получаем:

   

Далее находим

.

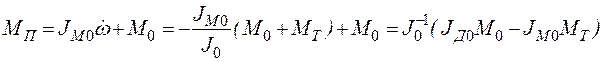Если выбрать M_T так, чтобы = 0, то момент M_П будет равен нулю в течение всего процесса торможения. Иными словами, передаточный механизм будет полностью разгружен. При этом 

.

Торможение машины может осуществляться двигателем. Такой способ торможения называется динамическим: его широко используют в современных электроприводах.

Глава 3.   КОЛЕБАНИЯ

Развитие конструкций современных машин, приборов и автоматов, в особенности в двигателестроении и в ряде технологических машин, отражает непрерывное повышение мощности и быстроходности при одновременном уменьшении веса. Как правило, динамическая нагруженность машин и их деталей увеличивается, роль динамических явлений возрастает. Среди всевозможных динамических явлений существенную роль играют колебательные явления.

В первую очередь следует отметить вредное действие колебаний. Значительная часть деталей машин (коленчатые валы, лопатки турбин, трубопроводы и др.) подвергается колебательным возбуждениям различными периодическими, почти периодическими или случайными силами, действующими самостоятельно или в сочетании с другими факторами (статической нагрузкой, температурой и др.) и при этом оказывается в состоянии значительной колебательной напряженности. Особую опасность представляют так называемые резонансные или критические режимы работы  элементов  машин  и конструкций,  при которых величина колеба-