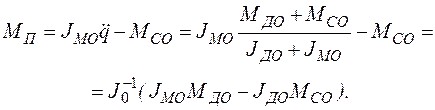Динамика жесткой машины с одной степенью подвижности, страница 23

                                                                                                              (2.102)

Зависимости М_П от угловой скорости машины можно найти, подставив в (2.102)  и .

Влияние динамической характеристики двигателя на разбег. Исследуем влияние динамической характеристики двигателя на разбег машины. Ограничимся случаем линейных характеристик (2.100). Пренебрегая в первом приближении влиянием возмущений, т.е. усредняя по q правые части уравнений (2.81), получаем:

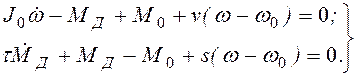                                                                                                              (2.103)

В этом случае, прежде чем начнется разбег машины, движущий момент должен достичь величины   (рис. 2.19). Нарастание момента М_Д должно происходить в соответствии с уравнением его динамической характеристики, в которой следует положить w = 0:

Интегрируя это уравнение при начальных условиях t = 0 и М_Д = 0, находим

.                                                                                                              (2.104)

Положив в (2.104) , найдем момент начала разбега

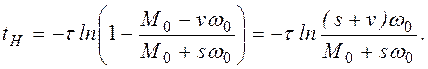
С этого момента разбег происходит в соответствии с уравнением (2.103). Если за начало отсчета времени принять этот момент, то следует искать решение, соответствующее начальным условиям t = 0; w = 0;  Определим М_Д из первого уравнения (2.103):

Отсюда

Подставив это выражение во второе уравнение (2.104), найдем

или                                                                       (2.105)

где                                      

Уравнение (2.105) необходимо решить при начальных условиях
w(0) = 0;     Последнее условие, очевидно, эквивалентно условию  Общее решение уравнения (2.104) представляем в виде суммы общего решения однородного уравнения

                                                                                                              (2.106)

и частного решения уравнения (2.105) . Для определения общего решения уравнения (2.106) составляем характеристическое уравнение

.

Корни этого уравнения

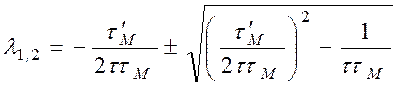
определяют характер переходного процесса.

Если >, то  и  - отрицательные вещественные числа. Общее решение уравнения (2.105) при этом имеет вид

.

Из начальных условиях следует, что

;    .

Отсюда находим

    .

Разбег в этом случае является апериодическим процессом, при котором

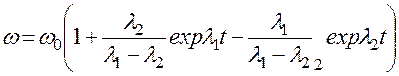.                                                                                                              (2.107)

Зависимость  для этого случая показана на рис. 2.20,а. При апериодическом разбеге  монотонно возрастает, стремясь к . При всех t будет <. Действительно, пусть 0>>; тогда  из (2.107) получаем

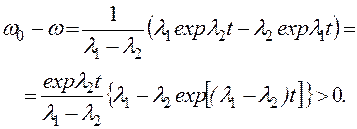
а)                                                 б)     

 

                                                        

 

0t0t

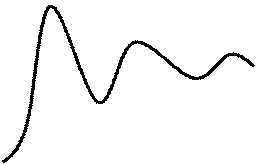
Рис. 2.20. Зависимости  при разбеге:

а – разбег – апериодический процесс;

б – разбег – колебательный затухающий процесс

Время разбега в первом приближении можно определить из
условия

или

.

При  0>> можно полагать, что <<.

Тогда

.

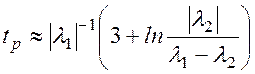Если <, разбег оказывается  затухающим  колебательным  процессом. При этом

      .

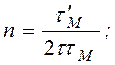
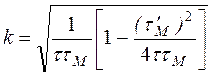Определяя общее решение уравнения (2.105) и используя начальные условия, получаем

                                                                                                              (2.108)

График  для этого случая показан на рис. 2.20,б. Максимальное значение  достигается при :

Таким образом, в этом случае при разбеге угловая скорость достигает значений, превосходящих скорость установившегося движения.