Динамика жесткой машины с одной степенью подвижности, страница 6

Решение этого уравнения q¹(t) примем за первое приближение
к искомому решению q(t). Далее, определив  и , подставим  q¹,  и  в правую часть уравнения (2.28) вместо q,  и . Получим уравнение

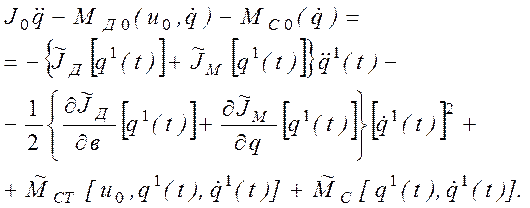
Решение этого уравнения будем рассматривать как второе приближение к искомому решению и т.д. Если итерационный процесс окажется сходящимся, т.е. если с ростом номера приближения s разность q^s(t)–q^s-1(t) будет стремиться к нулю при всех t, можно получить точное решение уравнения (2.25).

На практике, однако, обычно можно ограничиться первым приближением, которое в большинстве случаев дает точность, достаточную для технических задач.

Исследование нулевого приближения. Наметив общий путь решения задачи динамического анализа, перейдем теперь к его подробному рассмотрению. Как следует из изложенного, сначала определяются решения уравнения (2.26) в виде , которым соответствуют корни уравнения (2.27).

На рис. 2.4 показано, как можно решить это уравнение графическим методом. Для этого необходимо найти абсциссы точек пересечения функций  и - . Поскольку, вообще говоря, <0, график –  лежит выше оси абсцисс. При аналитическом задании функций М_Д0 и М_С0 решение может быть найдено одним из известных численных методов решения трансцендентных уравнений.

Как видно из рис. 2.4., графики могут иметь несколько точек пересечения (в данном случае две точки - А и В). Это означает, что уравнение (2.26) может иметь несколько решений вида , претендующих на нулевое приближение к искомому решению уравнения (2.25). Однако не все решения соответствуют реализуемым установившимся движениям системы, описываемой уравнением (2.26).

   М                                М_Д0

   М₀₁        А

                                                               arctg

   М₀₂

                                                               arctg

                -М_С0

       0     

Рис. 2.4. К определению средней угловой скорости

Рассмотрим, например решение , соответствующее точке А на рис. 2.4.  При случайном увеличении угловой скорости (>) момент движущих сил станет превосходить момент сил сопротивления; естественно, что при этом произойдет увеличение угловой скорости машины. Наоборот, при (<) движущий момент станет меньше, чем момент сил сопротивления, что вызовет дальнейшее уменьшение угловой скорости. Это свидетельствует о неустойчивости режима вращения с постоянной угловой скоростью . Легко убедиться с помощью аналогичных рассуждений, что вращение с угловой скоростью  (точка В на рис. 2.4) является устойчивым.

Продолжим исследование нулевого приближения. Выведем аналитическое условие устойчивости решения уравнения (2.26). Для этого рассмотрим поведение решения этого уравнения в окрестности исследуемого. Пусть

,                                                                                                                (2.30)

где     - малое приращение (вариация) решения.

Подставив (2.30) в (2.26) и сохранив в уравнении члены первого порядка малости, находим

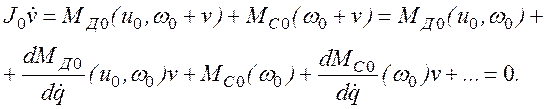
Учитывая (2.27), получаем уравнение для вариации :

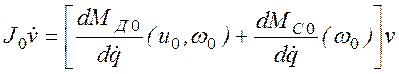.                                                                                                                (2.31)

В соответствии с (1.15)

,

где s – крутизна статической характеристики двигателя при .

По аналогии величину

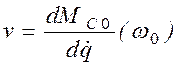                                                                                                                (2.32)

назовем крутизной среднего момента сил сопротивления. Уравнение (2.31) запишется в виде

.

Общее решение этого уравнения  стремится к нулю с ростом  t, если s + v>0. В этом случае, каким бы ни было малое начальное отклонение угловой скорости от значения , с течением времени угловая скорость будет стремиться к  и, следовательно, режим равномерного вращения с этой угловой скоростью будет устойчивым. Если же
s + v<0, то  возрастает с ростом t; при малом начальном отклонении угловая скорость будет с течением времени все более отличаться от ; режим вращения будет неустойчивым. Таким образом, условие устойчивости может быть записано в виде