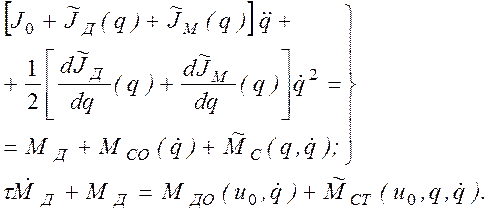Динамика жесткой машины с одной степенью подвижности, страница 17

                                                                                                                (2.80)

Так же, как и при учете статической характеристики, полагаем, что установившееся движение ротора мало отличается от равномерного вращения. Учитывая это, перепишем систему (2.80), перенеся в правую часть все явно зависящие от q члены, наличие которых вызывает неравномерность вращения ротора:

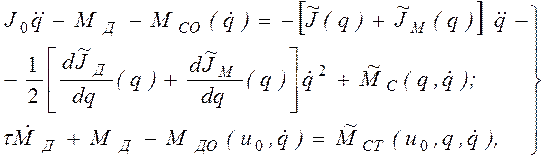                                                                                                                (2.81)

Приравняв нулю, левые части этих уравнений, получим систему:

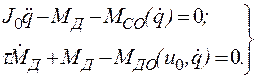                                                                                                                (2.82)

Решение системы имеет вид

;        ;                                                                                                                       (2.83)

и соответствует нулевому приближению к искомому решению. Подставив (2.83) в (2.82), получим уравнения:

                                                                                                                      (2.84)

из которых можно определить  и М₀. Исключая М₀ из уравнений (2.84), приходим к уравнению (2.27). Отсюда следует, что средняя угловая скорость ротора, определенная в нулевом приближении, не зависит от  и получается такой же, как и при учете статической характеристики. Она может быть определена из графика (см. рис. 2.5), причем ординаты точек пересечения характеристик соответствуют значениям среднего движущего момента М₀:

Определим условия устойчивости решений (2.83). Для этого введем малые вариации ; . Подставив их в (2.82), и, сохранив в этих уравнениях члены первого порядка малости, приходим к уравнениям:

       

Составив характеристический определитель для этой системы, получим

.

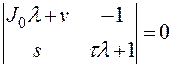Раскрывая его, имеем

.                                                                                                                (2.85)

Условием устойчивости (асимптотической) исследуемого решения является отрицательность вещественных частей корней уравнения (2.85), что обеспечивается, если его коэффициенты положительны. Отсюда получаем

 >0         >0.

Таковы условия устойчивости режима равномерного вращения: первое совпадает с (2.33); второе заведомо выполняется, если v >0. Только при v <0 (падающая характеристика среднего момента сил сопротивления) получаем дополнительное условие | v |  <J₀.

Определение динамических ошибок. Разыскивая далее решение системы (2.81) в виде

              

применяем метод последовательных приближений, аналогичный рассмотренному выше. Подставив решение (2.83), удовлетворяющее условиям устойчивости, в правые части уравнений (2.81), получим после линеаризации нелинейных характеристик по формулам (2.39) и (2.40) систему линейных уравнений с постоянными коэффициентами:

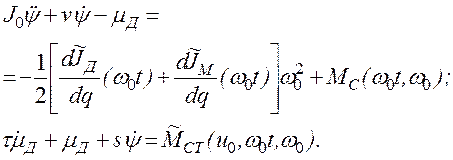
Запишем эти уравнения в операторной форме:

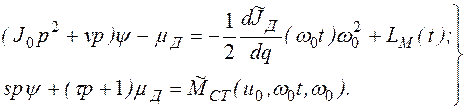                                                                                                                (2.86)

Рассматривая эти соотношения как алгебраические уравнения с неизвестными  и , получаем:

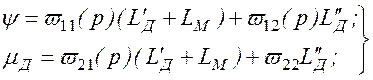                                                                                                                (2.87)

где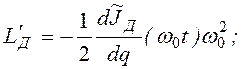                       

 

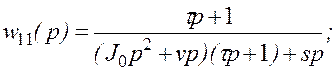
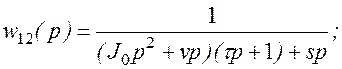
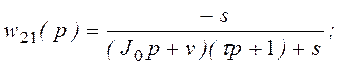
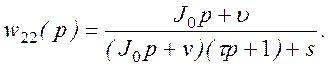
Ограничимся в дальнейшем случаем, когда источником возмущения является механическая система машины. Тогда  При этом из (2.87) получаем:

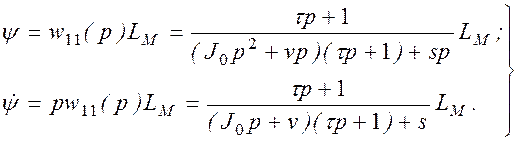                                                                                                                (2.88)

Используя представление  в форме (2.38), находим

 ;

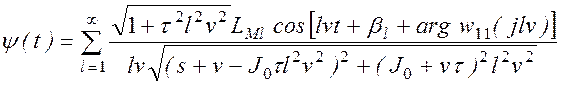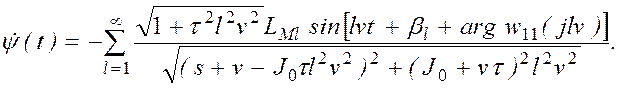
Исследование амплитудно-частотных характеристик. Исследуем более подробно динамическую ошибку по угловой скорости. С этой целью рассмотрим амплитудно-частотную характеристику

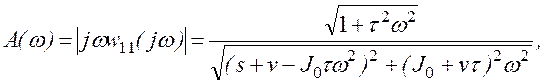
связывающую амплитуду  с амплитудой гармоники возмущения , имеющей частоту . Введем в рассмотрение параметр

                                                                                                                (2.89)

имеющий размерность времени и называющийся механической постоянной времени машинного агрегата. С учетом (2.89) имеем