Динамика жесткой машины с одной степенью подвижности, страница 19

Очевидно, что уменьшение момента, вызванного возмущением L_M(t), достигается при t_Д<t_М, t_Д+t_М>2t. При увеличении J_ДО величина t_Д растет сильнее, чем t_М, что, вообще говоря, приводит к увеличению момента. Увеличение J_MO  вызывает увеличение t_M и не увеличивает t_Д, что приводит к уменьшению момента . Здесь проявляются, таким образом, те же закономерности, которые обнаруживались при учете статической характеристики двигателя.

Для уменьшения максимальных значений   следует стремиться к сближению значений t_Д и t_М. Их равенство достигается при

Если t_Д + t_М >  2t, то и при t_Д <t_М, т.е. при J_ДОu<J_MOs, для всех значений w будет выполняться условие

Таким образом, согласованием параметров двигателя и механической системы агрегата можно обеспечить существенное уменьшение динамических нагрузок в передаточном организме. При малых значениях t(2t<t_Д + t_М) согласование сводится к выполнению условия

< ,                                                                                                                (2.92)

что может быть практически достигнуто либо увеличением крутизны характеристики двигателя s, либо уменьшением J_ДО.

При действии возмущения, идущего от двигателя (L_Д ¹0), условие согласования параметров (2.92) изменяется, как нетрудно показать, на противоположное.

2.10.  Исследование установившегося движения

с учетом сил трения в кинематических парах

До сих пор, анализируя динамику машинного агрегата, мы не включали в число сил сопротивления силы трения, возникающие в кинематических парах механизмов. Полный учет этих сил связан с отказом от использования уравнений Лагранжа второго рода, основанных на предположении об идеальности связей, наложенных на движение системы, т. е. об отсутствии трения в кинематических парах. При анализе механизмов с трением приходится в общем случае составлять уравнения движения каждого из звеньев механической системы машины (например, уравнения кинетостатики). Дополнив их характеристикой двигателя, можно получить систему уравнений движения машины, из которой определяются закон движения выходного звена двигателя, движущий момент и реакции во всех  кинематических парах. Естественно, что такой полный анализ целесообразен в тех случаях, когда есть основания полагать, что влияние сил трения на закон движения машины является существенным.

В ряде случаев существенные по величине силы трения возникают лишь в одной или нескольких кинематических парах. Это имеет место, например, при использовании в передаточном механизме червячной передачи. Метод решения задачи динамического анализа с учетом трения в одной кинематической паре и рассмотрен в этом параграфе.

Динамические модели кинематических пар с трением. Силы трения возникают, как известно, на поверхностях, по которым контактируют звенья, образующие кинематическую пару. Пусть S - поверхность соприкосновения  звеньев, образующих низшую кинематическую  пару (рис. 2.13). Выделим на этой поверхности в окрестности некоторой точки А элементарную площадку dS. В идеальной паре силы взаимодействия звеньев, образующиеся на этой площадке, сводятся к вектору dN, направленному по нормали к ней. В реальных низших кинематических парах возникает и касательная сила dF, вектор которой направлен противоположно вектору относительной скорости v_ск (скорости скольжения) в точке А. Сила dF является элементарной силой трения скольжения. Главный вектор сил трения F и главный момент этих сил относительно некоторой точки О определяются интегрированием элементарных сил и моментов по площади S:

;            .

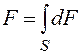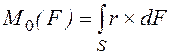                                                             A

                                              dS